Computer Vision - Ch.1~2

컴퓨터비전 공부 1일차

ComputerVision-오일석

Ch.1_2 컴퓨터 비전 문제는 어떻게 해결하나?

과학적인 접근과 공학적 접근

컴퓨터비전의 목표는 2가지입니다.

1. 사람의 시각에 맞먹는 인공 시각을 만든다.
2. 한정된 범위에서 특정한 임무를 달성하는 인공 시각을 만든다.
   

하지만 여기서 목표1은 현재 많은 어려움이 있는데,
예를들면 사람은 자연스럽게 자신이 보는 시야에서 어떠한 물체까지의 거리를 자연스럽게 파악하고, 그 과정에서 기하학적 변환(크기, 회전, 투영) 또는 광도 변환(조명, 그림자 등)이 있어도 자연스럽게 해석하는 반면 컴퓨터는 아직 그러한 알고리즘도 없고 쉽지가 않습니다. (이러한 1번 목표에 관한 관점이 과학적 접근입니다.)

1번 목표로 하기가 어렵다면 우회해서 부분적인 기능을 잘 해내는 방식으로 우회할 수 밖에 없습니다. 이러한 2번 목표에 해당하는 관점을 공학적인 접근이라고 합니다.

계층적 처리

컴퓨터 비전의 처리과정은 다음과 같습니다.

\[영상 - 전처리 - 특징추출 - 해석 - 고급묘사\]

특징추출까지를 저급비전이라하고 해석부분을 고급비전이라합니다.

특징추출(Feature Extraction) 은 영상에서 에지, 선분, 원, 코너, 텍스쳐 등의 특징을 추출하는 단계입니다.

컴퓨터비전에서 분석하고자하는 영상에 따라 어떤 특징을 사용할지 정하는 일이 매우중요합니다.

• 얼굴인식 : Harr-like(유사 하르)
• 사람탐지 : HOG(Histogram Of Gradient)
• 물체인식, 물체추적 : 예전에는 에지나 영역특징을 사용 요즘에는 SIFT, SURF 같은 지역 특징을 사용.
  

문제 해결 도구

컴퓨터비전의 문제들을 해결하기 위해 여러가지 해결 도구들이 있습니다.

• 자료구조와 알고리즘
• 수학
• 기계학습

등을 사용합니다.

시스템 설계

시스템 설계 과정은 다음과 같습니다.
문제 이해 - 데이터베이스 수집 - 알고리즘 설계와 구현 - 성능평가

챕터1은 개괄적인 요소들이 많으므로 간단히 훓고 넘어갔습니다.

Ch.2 영상 처리

디지털 영상이란?

획득과 표현

영상을 획득하는 장비인 카메라는 사람의 눈과 비슷한 구조를 가집니다. 수정체는 카메라의 렌즈역학을 하며, 망막은 CCD센서(필름)에 해당합니다.

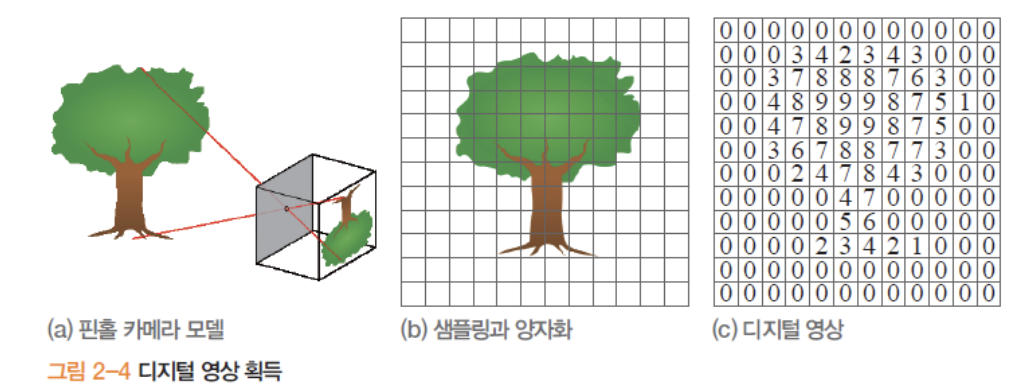
위 그림은 Pinhole(핀홀) 카메라 모델로, 복잡한 카메라의 작동원리를 단순하게 표현한 모델입니다. 빛이 상자에 있는 작은 구멍으로 들어가서 상이 뒤집힌채로 CCD센서에 맺힙니다.

CCD센서는 세로방향 M, 가로방향 N 개의 점으로 샘플링하고, 화소(Pixel)라고 부르는 각 점의 밝기를 L단계로 양자화(quantization) 합니다.

또한 영상처리에서 이제 우리는 기존에 알던 것과 조금은 어색하지만 익숙해져야할 부분이 있습니다.

2차원 영상 좌표계 에서 원점은 좌측상단에 위치해 있고, 행렬연산을 많이 사용할 것이기 때문에 우리가 익숙한 가로, 세로 순서가 아닌 세로, 가로 순서가 됩니다.

또한 0부터 카운트하기 때문에,

• 최대 화소는 M-1, N-1 까지가 됩니다.
• 해상도는 $M \times N $
• 명암의 범위는 [0~L-1], 보통 L=256
• L=2이면, 이진영상
• 컬러영상은 $f_{r}(x), f_{g}(x), f_{b}(x)$ 로 3가지를 가집니다. r(Red), g(Green), b(Blue)
  

히스토그램

히스토그램 계산과 용도

히스토그램은 어떤 명암의 픽셀이 얼마나 분포해있는지 보기에 편안한 그래프입니다.

가로축은(0~256) 명암도를 나타내고, 세로축은 그 명암도를 가진 픽셀의 개수를 나타냅니다. 즉 히스토그램의 왼쪽부분의 그래프가 높으면 어두운 사진을 오른쪽편에 그래프가 높으면 밝은 사진을 나타내는 것입니다.

또한, 모든 히스토그램의 칸을 더하면 1이 되는 정규 히스토그램 은 다음과 같습니다.

\[\hat{h}(l) = \frac{h(l)}{M \times N}\]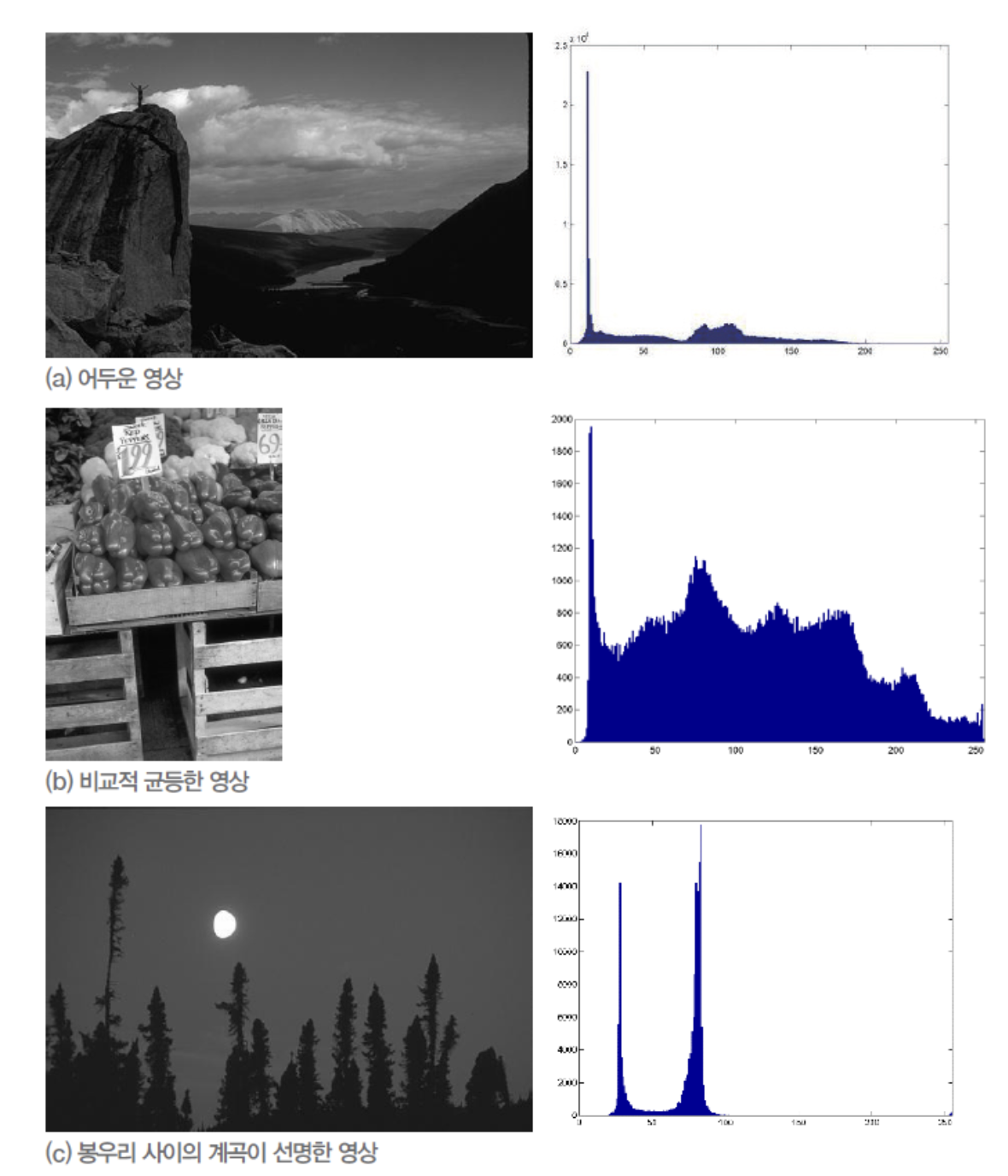

뒤에서 더 다루겠지만 (C) 그림과 같이 한 눈에 보아도 두 픽셀의 분포가 높은 사진은 이진화하기 쉬운 사진이라고 할 수 있습니다.

히스토그램의 또 다른 역할은 조작을 통한 영상 품질의 개선입니다. 가장 대표적인 연산은 히스토그램 평활화 입니다.

히스토그램 평활화를 하게 되면 비교적 모여있는 명암의 화소들을 넓게 펴주어 명암의 범위를 넓혀줍니다. 즉, 동적 범위가 늘어나 영상이 이전보다 선명해집니다.

• c() : 누적 히스토그램
• round() : 반올림 연산
• T() : 입력 영상 f의 명암값 $l_{in}$ 을 출력영상 g의 명암값 $l_{out}$ 으로 변환하는 매핑 함수.
  

\[l_{out} = T(l_{in}) = round(c(l_{in})\times(L-1))\] \[여기서 c(l_{in}) = \sum^{l_{in}}_{l=0} \hat{h}(l)\]

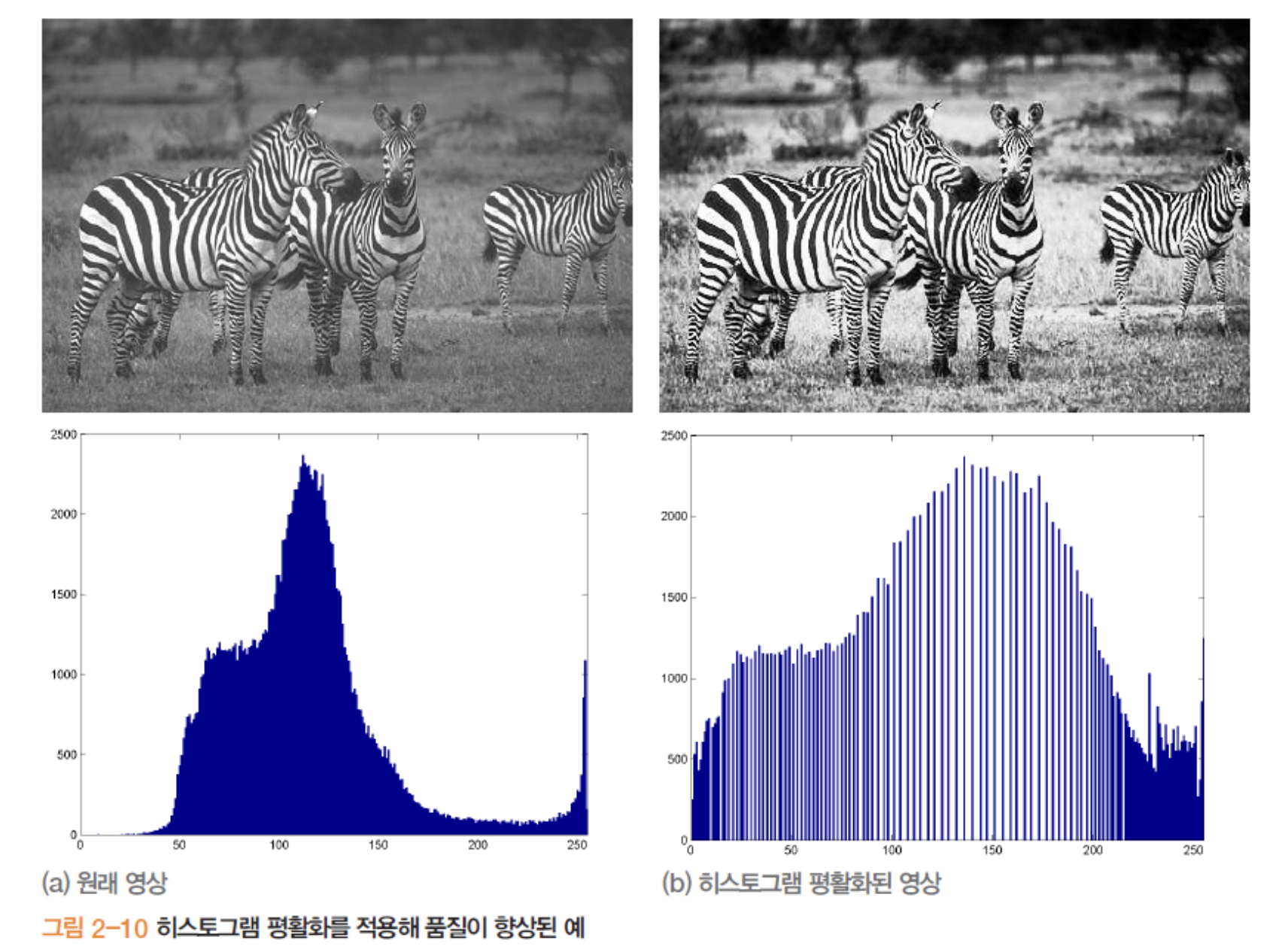
히스토그램 평활화덕분에 얼룩말이 선명하게 보이는 것을 볼 수 있습니다.

반면에 이번에는 히스토그램 평활화를 했더니 오히려 품질이 떨어진 예입니다. 새의 깃털의 텍스쳐도 훼손되었으나, 새에게 먹히는 곤충을 확인하는 목적이라면 평활화한 영상이 더 적합하다 할 수 있습니다.

히스토그램 역투영과 얼굴 검출

일반적인 사진의 경우, 명암이라는 한가지 요소로만 이용하면 얼굴과 같은 사진에서 비슷한 명암을 갖는 다른 영역이 여러군데 존재할 가능성이 높아서 얼굴을 구별하기 어렵게 됩니다.

그러므로 RGB 색상 공간을 HSI 공간으로 변환한 다음, I채널(명암)은 무시하고 H채널(색상)과 S채널(채도)를 사용합니다

간단히하면, H와 S채널의 값이 높을 수록 얼굴일 확률이 높아진다라는 의미입니다. 대신 이 방법은 얼굴색과 유사한 배경이 없다는 가정하에 효율적인 방법입니다.

이진 영상

우리는 때때로 영상을 흑과 백으로 이루어진 이진 영상으로 바꿀 필요가 있습니다.

이진화와 오츄 알고리즘

앞에서 이진 영상을 살짝 소개하면서 뒤쪽에서 더 자세히 다룬다고 한 내용 기억나시나요?

딱 눈에 보이게 두개의 명암으로 분리되는 사진이나 영상이 아니라면 어떻게 이진 영상으로 변환할 수 있을까요?

정답은 어떠한 임계값을 기준으로 그 기준보다 낮으면 흑으로 높으면 백색으로 바꾸는 것입니다. 수식은 다음과 같습니다.

\[b(j,i) = \begin{cases} 1, & f(j,i) \geq T \\ 0, & f(j,i) < T \end{cases}\]

엇! 그렇다면 결국 두 구간을 나누는 임계값 T(threshold) 가 필요한데, 한눈에 나눠야하는 곳이 보이지 않는다면 어떻게 해야할까요?

이 질문의 해답이 바로 오츄 알고리즘 입니다.

임계값 t를 기준으로 나누었을 때, 각 집합의 명암 분포가 균일할수록, 즉 분산이 낮을수록 높은 점수를 주어서, 가능한 모든 t에 대해서 점수를 계산한 후 가장 좋은 t를 최종 임계값으로 정하는 것이 바로 오츄 알고리즘입니다. 일종의 최적화 알고리즘입니다.(optimizaion algorithm)

최적화 알고리즘을 계산하는데 사용하는 함수를 목적함수(objective function) or 비용함수(cost function)이라 부릅니다. 딥러닝의 손실함수와 비슷한 개념이네요!

위의 예시에서 분산이 작을수록 균일성이 크므로, 목적함수값이 작을수록 점수가 높다고 셍각하여야합니다. 딥러닝처럼 손실이 최소화되는 그 지점을 찾아야하는 것처럼 말이죠.

아래식은 오츄알고리즘의 핵심입니다. \(T = argmin \ v_{within}(t) \\ t \in \{0,1, \cdots , L-1\}\)

교재에는 분산과 평균 그리고 상수처리할 수 있는 점들을 이용하여 간단히하는 부분이 나와있는데, 수식의 압박이 상당하기 때문에 궁금하신 분들은 따로 찾아보시길 추천드립니다.

공부를 더 해보면서 중요한 수식이라 생각이들면 추후 추가수정하겠습니다.

위 사진은 오츄알고리즘에 의해 컴퓨터가 찾아준 임계값으로 이진 영상처리한 사진입니다. (b) 사진은 가격표가 제대로 보이지 않고, (c) 사진은 달이 보이지 않는 문제점이 발생하였습니다.

이를 해결하려면 임계값을 k개 사용하여 k+1개의 구간으로 구분하는 다중 임계값 방법을 사용해야 합니다. 이는 5장에서 다시 다루겠습니다.

연결요소

화소는 어떤 모양을 사용할까요? 만일 원모양을 사용한다면 원과 원사이의 빈공간을 해결할 수 없고, 6각형을 사용한다면 좌표계로 딱 정의하기 어렵다는 단점이 있어서 사각형을 사용합니다.

사각형끼리 맞닿아 있을 때, 동서남북 4개의 화소를 이웃으로 간주하는 4-연결성과 주위를 둘러싼 여덟 개 화소를 모두 이웃으로 삼는 8-연결성 두가지가 있습니다.

영상 처리의 세 가지 기본 연산

영상 처리란, 기존의 화소에 새로운 값을 대입해준다 라고 생각할 수 있습니다. 소개되는 방법들 이외에 다른 여러가지들도 모두 이 3가지에 해당됩니다.

먼저 점 연산 은 자신의 값만 보고 새로운 값을 결정한다 라고 보시면 되겠습니다.

영역 연산 은 이웃에 있는 몇 개의 화소들을 보고 새로운 값을 결정하는 방식입니다.

마지막으로 기하 연산 은 일정학 기하학적 규칙에 따라 다른 곳에 있는 값을 취하는 방법입니다.

점 연산

점 연산의 기본적인 식은 다음과 같습니다.

\[f_{out}(j,i) = t(f_{1}(j,i), f_{2}(j,i), \cdots , f_{k}(j,i))\]

위의 식은 대부분 한 장의 영상을 입력값으로 줍니다.

이제, 영상을 밝거나 어둡게 그리고 반전을 줄 수 있는 선형 연산(Linear operation 은

\[f_{out}(j,i) = t(f(j,i)) = \begin{cases} min(f(j,i)+a,L-1), & (밝게) \\ max(f(j,i)-a,0), & (어둡게) \\ (L-1)-f(j,i), & (반전) \end{cases}\]

a는 양수입니다. 밝게는 양수값 a부터 L-1범위까지 명암을 더해주니 당연히 밝아지는 것이고, 어둡게는 a부터 0까지의 범위를 빼주니 당연히 어두워지는 원리 입니다. 반전은 최대 명암값에서 기존화소의 명암값을 빼주니, 검정배경의 경우를 예로들면 최대명암값에 검정의 명암값 0이 빠지니 반대로 하얀색 배경이 되는 것입니다.

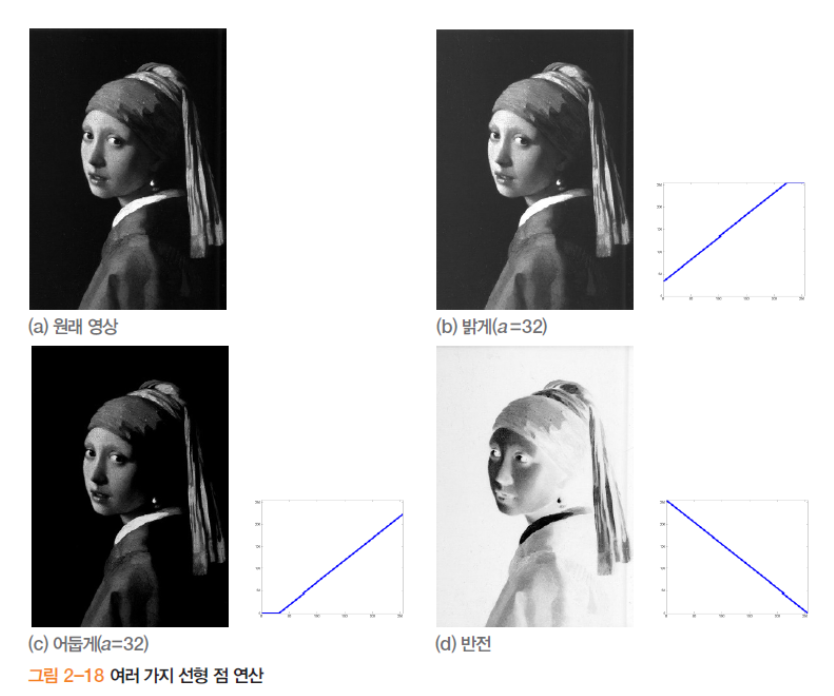
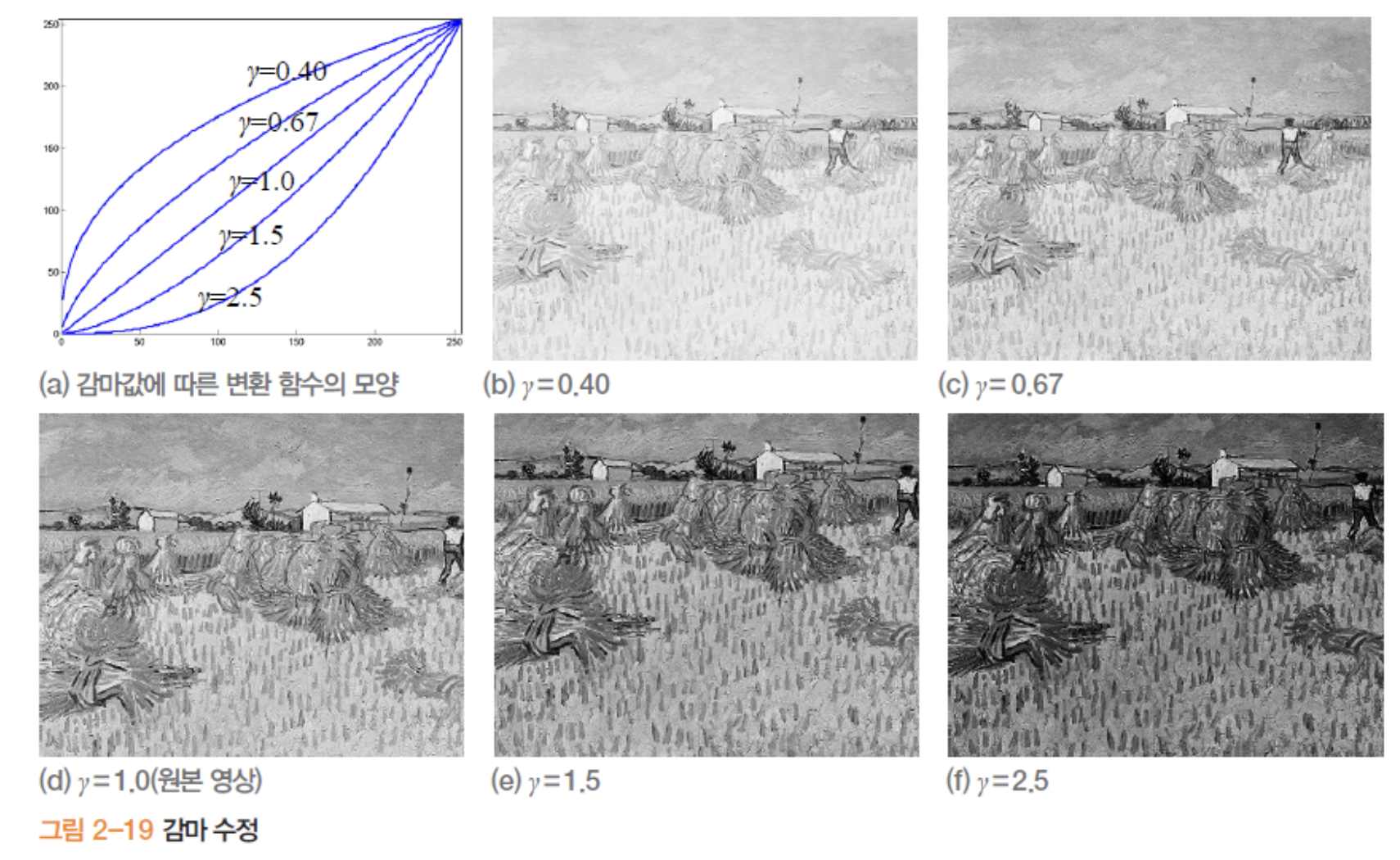
위에까지는 선형 연산이였습니다. 이제는 비선형 연산(Nonlinear operation) 이라 불리는 감마 수정(Gamma correction) 에 대해서 알아보겠습니다.

$\hat{f}$ 은 [0,1] 사이의 값을 가지는 정규 영상입니다.

\[f_{out}(j,i) = (L-1) \times (\hat{f}(j,i))^\gamma\] \[여기서, \hat{f}(j,i) = \frac{f(j,i)}{(L-1)}\]

감마값에 따라서 영상이 달라지는 감마 수정입니다. $\gamma$ 가 1보다 크면 0~1사이의 값을 거듭제곱해주므로 어두운 영상이 나오게 되고 반대로 1보다 작으면 밝은 영상이 나오게 됩니다.

디졸브 파워포인트같은 곳에서 자연스럽게 장면 전환이 되는 것을 디졸브라고 합니다. 디졸브연산도 점연산중에 하나입니다. 일반적인 영상은 R,G,B 세 채널이 입력되므로 영상의 개수 k=3입니다.

k=2인 디졸브의 수식은 아래와 같습니다.

\[f_{out}(j,i) = \alpha f_{1}(j,i) + (1-\alpha)f_{2}(j,i)\]

영역 연산

영역연산에서 중요한 역할을 할 두 가지 연산인 상관(correlation) 과 컨볼루션(convolution) 에 대해서 알아보겠습니다. 윈도우 u는 검출하려는 물체영상이고, f는 입력 영상이라고 합시다. 풀어야할 문제는 f의 어디에 u가 있는지 찾는 것입니다.

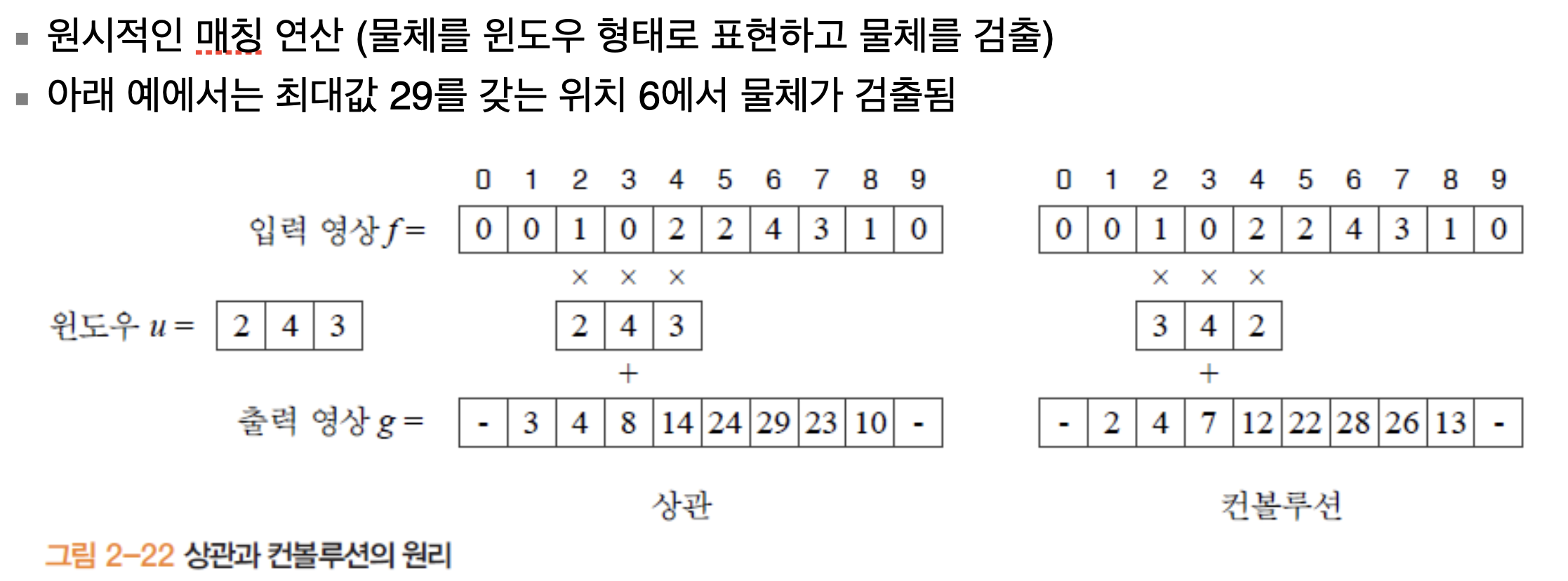
CNN에서의 컨볼루션 연산과 거의 동일합니다. 윈도우가 지나가면서 그림에서처럼 (1x2)+(0x4)+(2x3)=8 이라는 연산 값이 중앙에 있는 블럭 아래로 들어가게 됩니다. 그렇기 때문에 상관과 컨볼루션 연산에서는 윈도우가 짝수인 것은 사용하지 않고 편의상 홀수로 합니다.

컨볼루션과 상관의 차이는 윈도우가 뒤집어지냐 아니냐의 차이입니다.

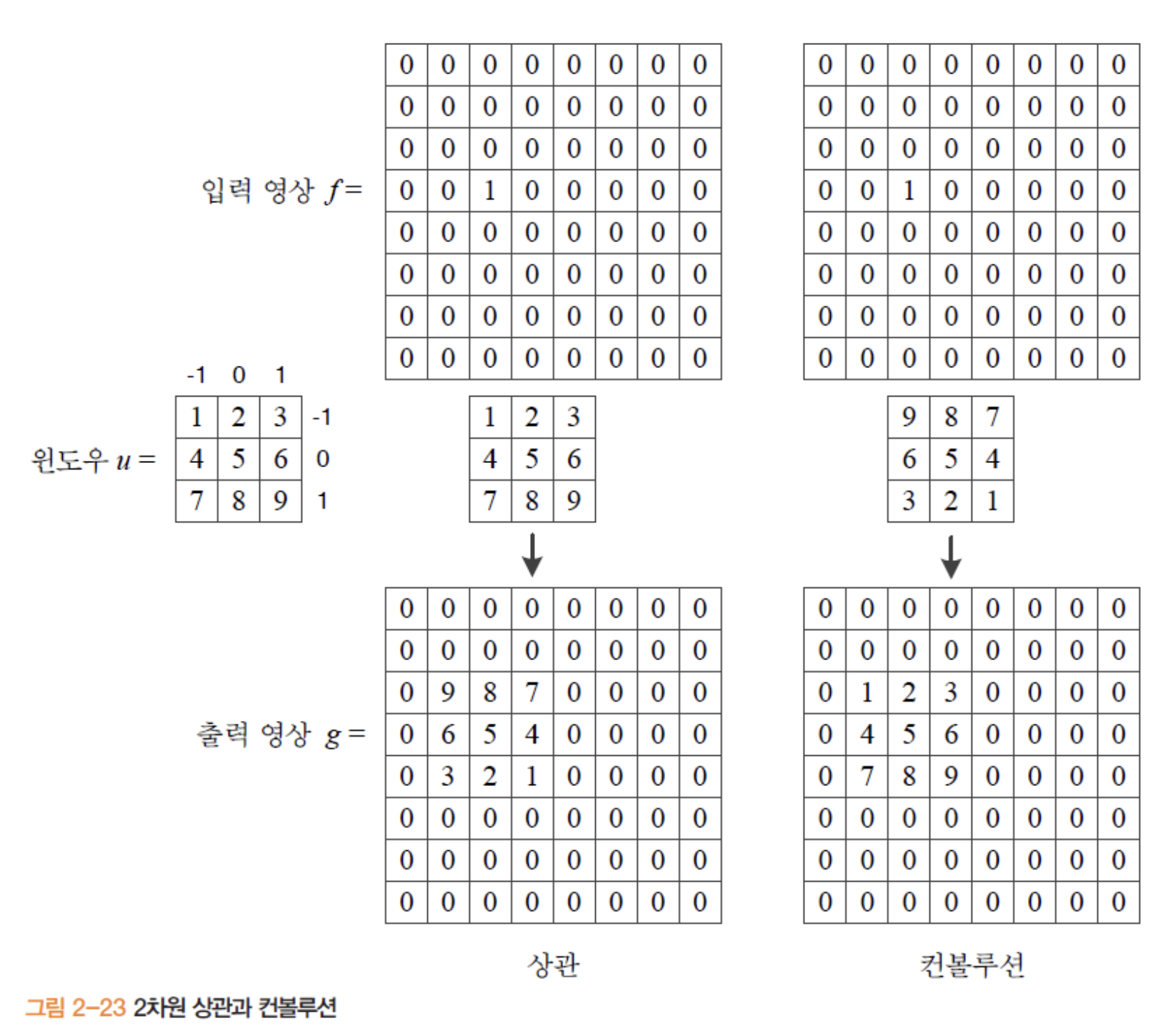
그림을 보면 (3,2)만 1을 갖고 나머지는 0을 가지는 영상과 3x3 크기의 윈도우가 있습니다. 이러한 영상은 크기가 1인 자극이 한 곳에만 나타나므로 단위 임펄스(unit impulse) 라 부릅니다.

상관의 경우 윈도우가 뒤집어진 모양이 결과영상으로 나오지만, 컨볼루션의 경우 u가 그대로 나타납니다. 따라서 컨볼루션에서는 임펄스 함수에 그대로 반응한다는 뜻으로 윈도우를 임펄스 반응 함수(impulse response fuctino) 라고 부르기도 합니다.

컨볼루션은 그 자체가 특정 목적을 갖는게 아니라 마스크의 모양과 크기가 정해지면 특정효과가 결정됩니다. 그러한 마스크중에 박스(box) 는 단순히 아홉개 화소의 평균을 구해주어 모든 화소값의 합이 1이 나오도록 정규화해줍니다. 이는 정규 마스크라 부르는데, 결과 영상의 화소값이 원래 영상과 비슷한 범위를 가집니다.

가우시안 마스크는 표준편차가 0.5일 때 입니다. 그래서 화면 엣지쪽으로 갈수록 영상이 희미해집니다.

박스나 가우시안과 같은 연산을 스무딩 연산이라 부르고, 주로 영상 향상 작업에 많이 사용합니다. 왜냐하면 보통 노이즈라하는 영상의 잡음들은 어떤 화소가 다른 화소에 비해 유난히 크거나 작을 때 발생하는데, 박스나 가우시안은 이 화소와 이웃 화소의 차이를 줄여주기 때문입니다.

샤프닝은 스무딩과 반대로 작용하는 것을 말합니다.

비선형 연산, 메디안(median)

메디안 필터는 영상의 화소(j,i)에 hxw 크기의 마스크를 씌우고 그 속에 있는 화소들의 메디안, 즉 중간값을 결과로 취합니다. 그렇기에 메디안필터도 가우시안이나 박스처럼 스무딩 연산에 속합니다.

메디안 필터는 솔트페퍼 잡음(salt-pepper noise) 제거에 매우 효과적입니다.

가우시안필터와 메디안필터의 차이는 무엇일까요? 가우시안필터와 메디안필터는 물체의 경계부근에 차이가 있습니다. 가우시안은 물체의 경계 부근에 대비가 훼손되어 나타나지만, 메디안은 상대적으로 대비를 잘 유지한 것을 볼 수 있습니다.

가우시안필터로 잡음을 더 제거하기 위해 필터의 크기를 키우게되면 그만큼 에지가 뭉개지는 현상이 심해지게 됩니다. 이러한 특징 때문에 메디안을 에지 보존(edge preserving) 스무딩필터 라고 합니다.

메디안필터는 시간이 오래걸린다는 단점이 있습니다. 메디안필터보다 뛰어난 에지 보존 필터는 양방향필터나 쿠와하라필터가 있습니다.

기하 연산

점 연산과 영역 연산은 자기 자신 또는 자기 이웃에 있는 화소에 영향을 받는 방법이었습니다. 하지만 영상을 회전하거나 특정 부분을 확대 축소 하는 등의 작업이 필요한 경우는 멀리 떨어져있는 화소값도 고려해야합니다. 이 경우 기하 연산을 사용합니다.

동차 좌표와 동차 행렬

기하 변환은 동차 좌표(homogeneous coordinate) 와 동차 행렬(homogeneous matrix)로 표현합니다. 2차원 좌표는 3차원으로 확장 할 때, 새로운 차원값에 1을 추가해주면 됩니다. 이렇게 확장된 벡터는 기존 벡터와 구분하기 위해서 문자 머리에 점으로 표시합니다.

$x=(y,x) \to \dot{x} = (y,x,1)$

동차 행렬은 변환 목적에 따라 다음 사진과 같이 제시한 종류 중 하나가 됩니다. 크기는 3x3 입니다.

사실 회전변환 행렬은 x축을 기준으로도, y축을 기준으로도 회전할 수 있으나, 그것은 선형대수에서 사용하는 개념이고 영상을 회전시킨다는 것은 어떻게 보면 우리가 원점으로 보고 있는 그 점이 z축을 우리가 수직으로 보아서 점으로 보고있고 그 z축을 기준으로 회전 하면 영상이 회전이 되는 원리입니다.

그리고 이러한 행렬의 연산은 매번 계산하지 않아도 되는 이점이 있습니다. 복합 변환(composite transformation) 을 이용하면 매번 k단계의 변환이 이루어져야하는 상황에 k배 만큼 빠르게 연산할 수 있습니다.

아래 사진을 통해 쉽게 이해하실 수 있습니다.

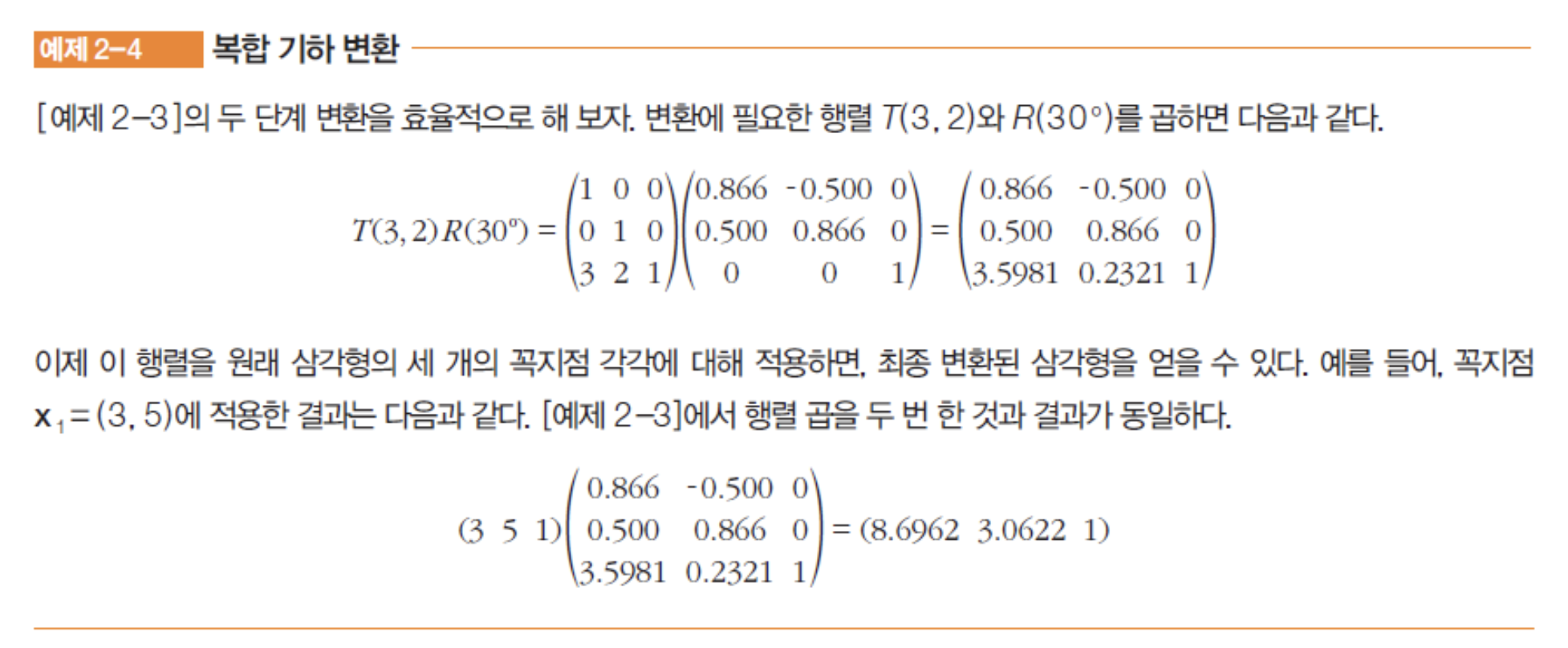
이러한 복합 변환을 이용하여, 원점을 중심으로 회전하는 것이 아니라 어떠한 점 $(y_{c},x_{c})$ 를 기준으로 회전하고 싶다면 어떻게 해야할까요?

바로 그 점을 원점으로 평행이동하는 행렬과 회전행렬 그리고 다시 그 점의 위치만큼으로 이동시키는 행렬을 순차적으로 곱한 행렬을 구해서 연산해주면 됩니다!

$T(-y_{c},-x_{c})R(\theta)T(y_{c},x_{c})$

이런 원리로 어떠한 연산도 가능합니다. 이러한 변환들을 통칭하여 어파인 변환(affine transformation) 이라 부릅니다. 이러한 어파인 변환은 마지막 열이 항상 $[0,0,1]^T$ 를 가집니다. 이 열이 달라지면 어파인 변환이 아닙니다. 예로 투영 변환이 있습니다.

영상에 기하 변환 적용

예제[2-3]에서 얻은 좌표가 (8.6962, 3.0622) 인데 이를 반올림하여 (9,3)으로 하면 어떻게 될까요?

이렇게 영상을 처리하게되면 어떠한 화소는 값을 받지 못하는 현상이 발생하고 이는 시각적으로 불만족스러운 현상이 생깁니다. 이를 통틀어 에일리어싱(aliasing) 이라고 부르고 이러한 현상을 해소하는 노력을 안티 에일리어싱(anti-aliasing)

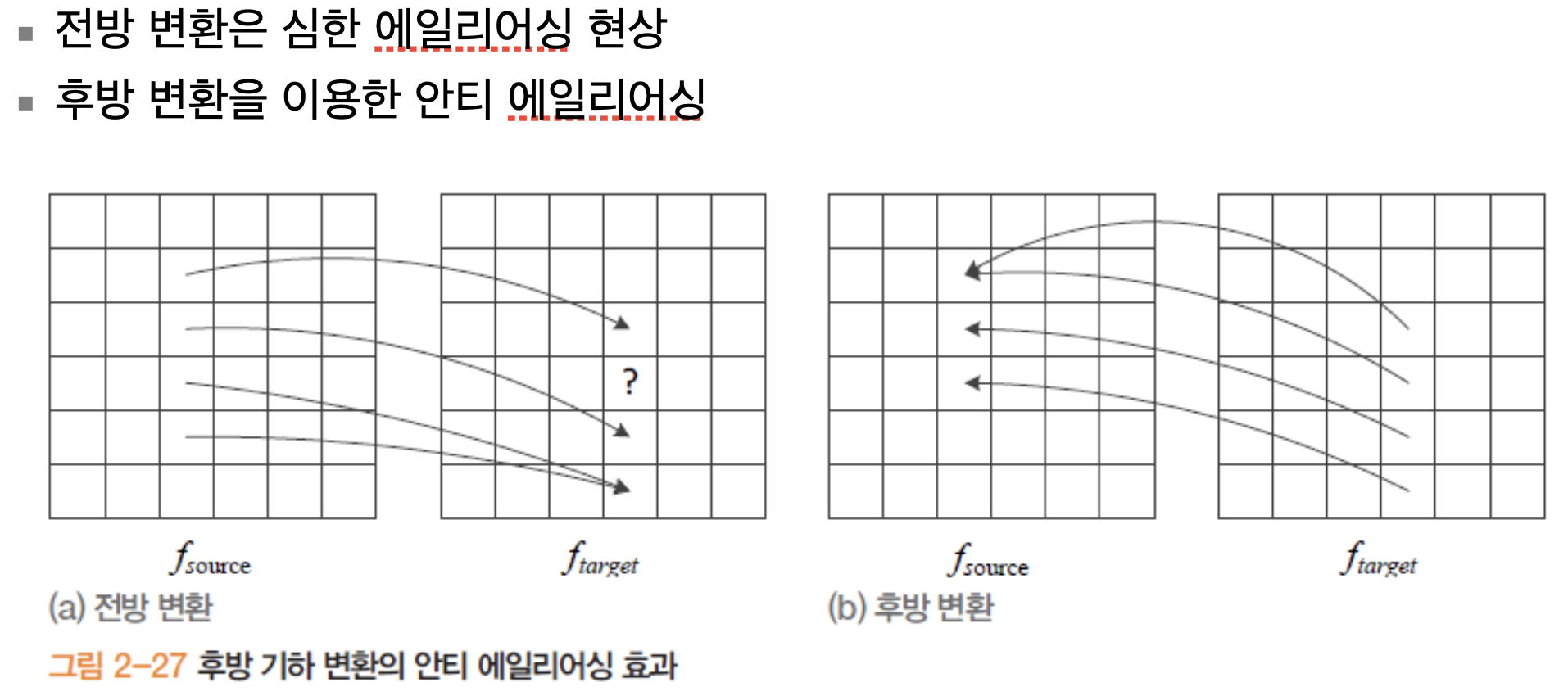
위 그림에서의 안티 에일리어싱 알고리즘의 원리는 빈 공간이 생긴 화소는 역행렬을 이용하여 역변환을 취해 원래 화소값을 찾아서 매꿔주는 원리입니다.

양선형 보간

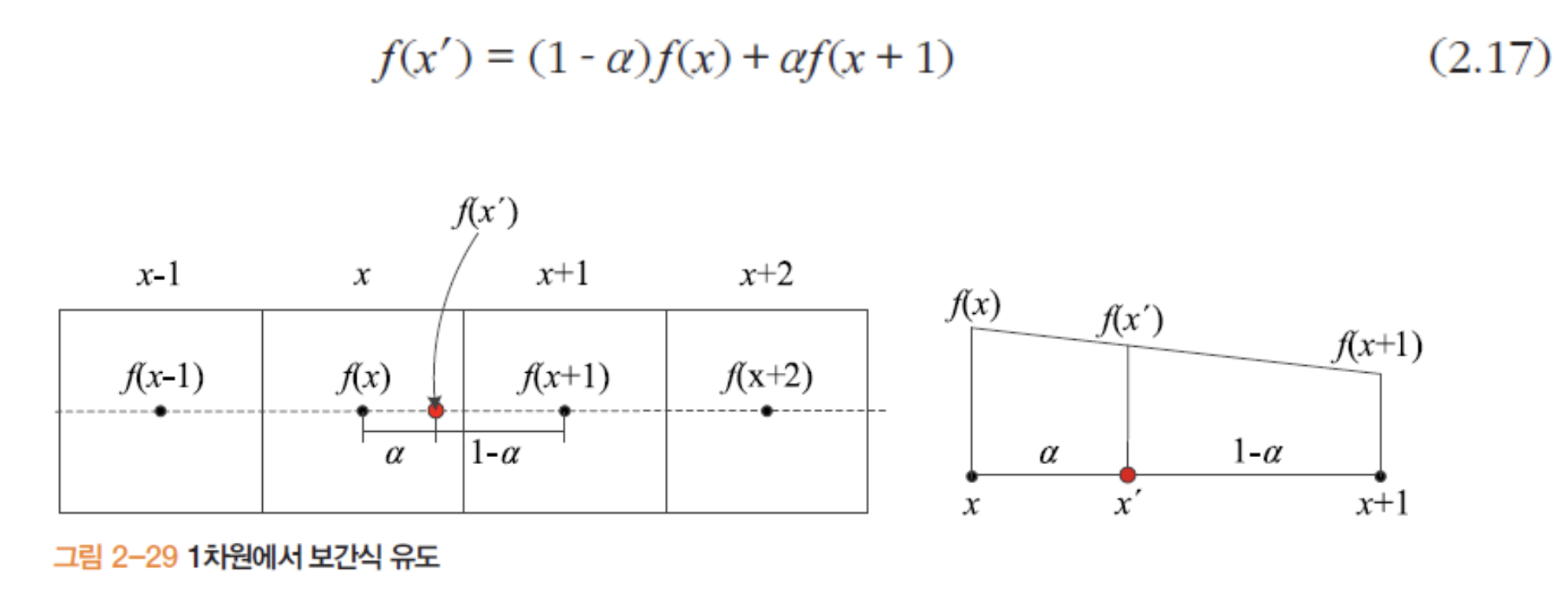
이렇게 역변환만으로 에일리어싱을 완전히 없앨 수 있을까요? 정답은 아닙니다. 왜냐하면 목표 영상의 여러 점이 원래 영상의 같은 점을 참조할 수 있으므로 여전히 에일리어싱은 남는 문제가 생깁니다. 이러한 문제를 해결할 수 있는 더 효과적인 방법이 보간(interpolation) 입니다.

2차원을 1차원으로 낮춰서 간단히 보간에 대해 설명하면, 바로 옆 두 화소 명암의 적절한 차이를 이용하는 방법입니다.

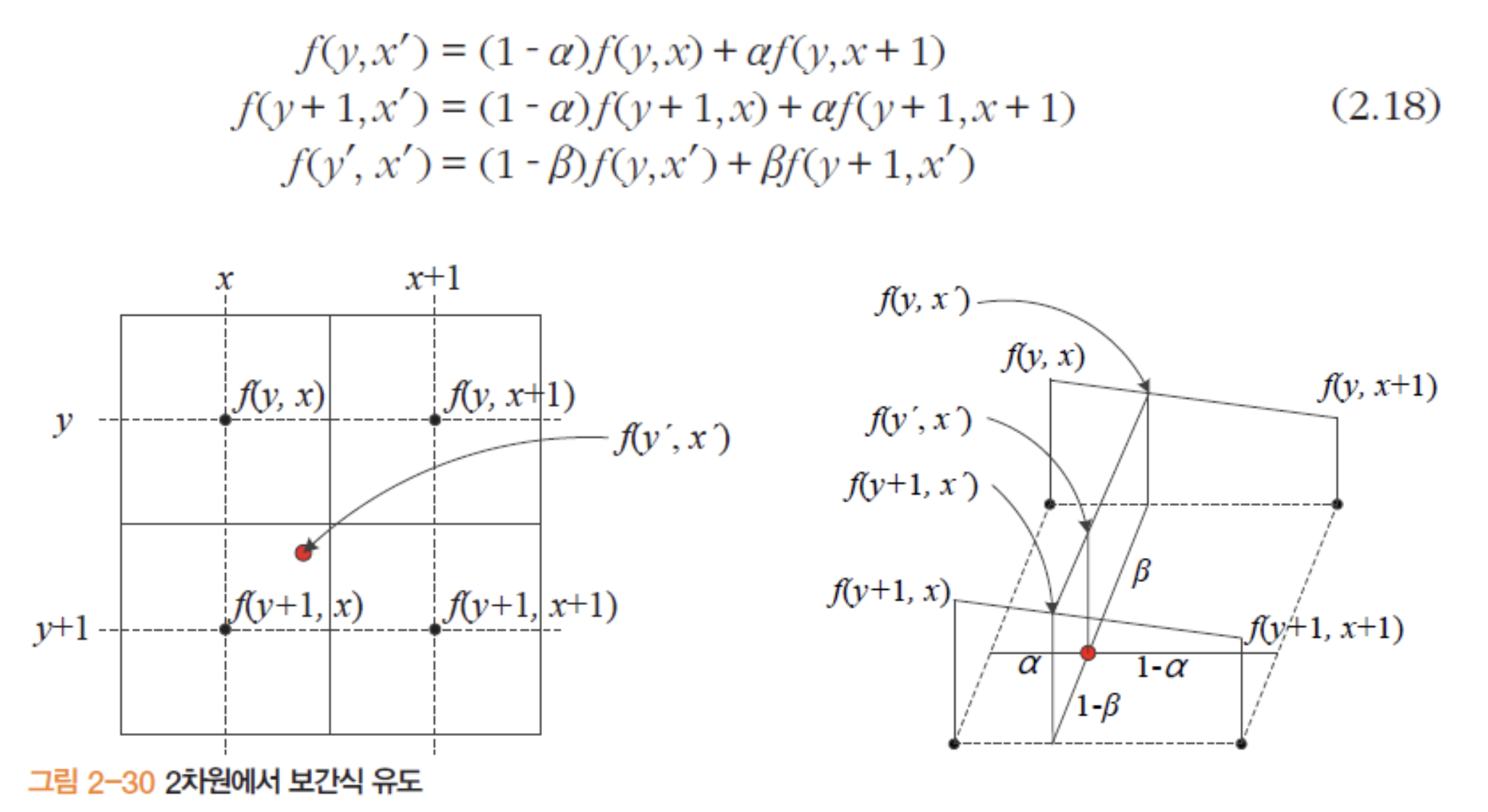
이제 2차원으로 확대해서 생각해보면 인접한 화소가 4개로 늘어납니다. 위의 1차원식을 여러번 반복하여 구합니다.

먼저, y행에서 x방향으로 보간식을 적용하여 $f(y,x’)$ 를 얻고, 같은 과정을 y+1행에 적용하면 $f(y+1, x’)$ 을 얻을 수 있습니다. 그 다음 얻은 $f(y,x’)$ 와 $f(y+1, x’)$ 를 이용하여 y방향으로 보간식을 적용하면 $f(y’, x’)$ 를 최종적으로 구할 수 있습니다.

위와 같은 방법은 그냥 제일 가까운 점의 명암값을 취하는 최근접 이웃(nearest neighbor) 방법보다 계산 시간은 길지만 영상의 품질은 훨씬 뛰어납니다.

이 기법은 선형보간(linear interpolation)을 이용하는데 두 방향에 걸쳐 수행하므로 양방향 선형 보간(bilinear interpolation) 방법이라 부릅니다. 추가적으로 다른 방법으로는 비선형 보간 방법으로서 양 3차 보간(bicubic interpolation) 기법도 있습니다. 이 기법은 16개의 이웃 화소와 3차 함수를 이용합니다.

다해상도

지금까지 앞에서 공부한 부분들은 해상도가 정해져있는 환경이였습니다. 하지만 우리는 노트북에서 모니터 혹은 패드 휴대폰 등등 해상도가 커지고 작아져야하는 상황들이 있습니다.

이 때, 해상도를 늘리는 것을 업샘플링(upsampling) , 내리는 것을 다운샘플링(downsampling) 이라 부릅니다.

컴퓨터비전의 목표는 다양하게 변화된 상황에 상관없이 물체를 안정적으로 찾아내고 인식하는 것입니다. 그래서 고안된 기법이 영상 피라미드(image pyramid) 입니다.

아래 그림과 같이 피라미드는 해상도가 다른 여러장의 영상으로 구성됩니다. 이를 다중 해상도(multi-resolution) 영상이라 부릅니다. 이러한 구조는 거침과 세밀함(coarse-to-fine) 처리 방식을 사용합니다. 저해상도의 거친 영상에서 물체의 대략적인 위치와 모양을 찾고, 고해상도에서 세밀하게 물체의 정확한 위치와 모양을 결정합니다.

하지만 단순히 다운샘플링을 0.5 비율로 계속 진행한다면 심각한 에일리어싱 발생하게됩니다. 왜냐하면 짝수 좌표의 화소는 100% 반영되지만, 홀수 좌표의 화소는 0% 반영되기 때문입니다.

버트와 아델슨은 이러한 문제를 해결하기 위해 Burt83a 라는 해결책을 제시하였습니다. 이 방법은 다운샘플링을 하기전에 스무딩을 적용하는 것입니다.

모폴로지

이진 모폴로지

컴퓨터비전에서 영사에 나타난 물체의 모양을 분석하거나 원하는 형태로 바꿀 때 자주 사용하는 연산입니다. 모폴로지는 명암 모폴로지 와 이진 모폴로지 로 나뉩니다.

모폴로지는 구조요소(structuring element)를 사용하여 이진 영상에 있는 연결요소의 모양을 조작합니다.

이제 가장 기본적인 두 가지 모폴로지 연산인 팽창(dilation) 과 침식(erosion) 에 대해서 알아봅시다.

팽창은 f의 1인 화소에 구조요소 s를 씌우고 s의 1인 점과 겹치는 곳을 모두 1로 바꿉니다(합집합). 결과적으로 영상에 있는 연결요소는 구조요소만큼 외부로 팽창합니다.

반대로 침식은 f의 어떤 화소에 구조 요소를 씌었을 때 구조요소의 1인 곳과 겹치는 곳이 ‘모두’ 1인 경우만 그 화소를 1로 결정합니다(교집합).

\[팽창 : f \oplus S \\ 침식 : f \ominus S\]

위처럼 표시합니다. 여기서 열기, 닫기 연산은 팽창과 침식을 둘다 사용합니다.

\[열기 : f \circ S = (f \ominus S) \oplus S \\ 닫기 : f \bullet S = (f \oplus S) \ominus S\]

위 식에서 알 수 있듯이 열기는 침식후 팽창, 닫기는 팽창 후 침식 연산을 사용합니다.

명암 모폴로지

….test