Lec 02,03: Linear Regression

딥러닝 공부 3일차

Linear Regression

• Data definition, 데이터 수집
• Hypothesis, 가설 수립
• Compute Loss, 손실계산
• Gradient Descent, 경사하강법
  
  

  Data Definition

훈련 데이터셋과 테스트 데이터셋

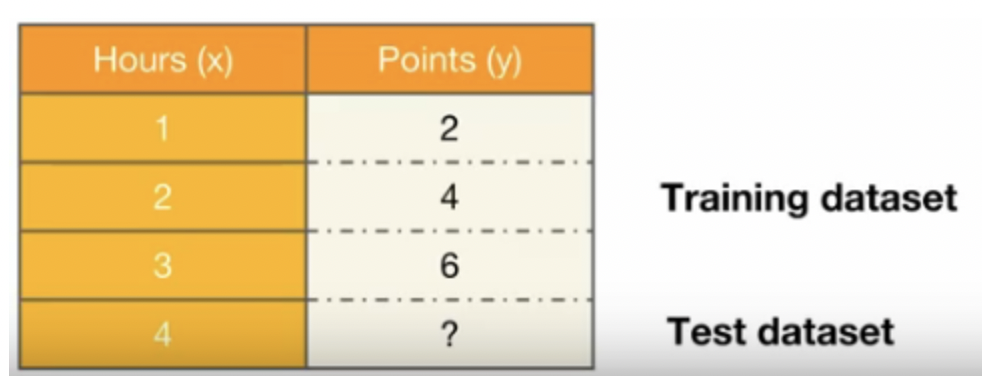
공부한 시간에 비례해서 점수가 나온다고 했을 때 4시간 공부하면 몇점을 얻을 수 있는가? 에대한 데이터입니다.

훈련 데이터셋은 입력과 출력으로 나뉘는데 이는 파이토치의 텐서의 형태로 이루어져있어야합니다.

여기서 x_train은 공부한시간 y_train은 점수입니다.

x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [5], [9]])

저는 교재 예제에서 숫자를 조금 바꿔서 응용해보겠습니다.

Hypothesis 수립

선형회귀에서 가설은 직선의형태이고 그 중 학습데이터와 가장 유사한 직선을 찾아야합니다.

\[y= Wx+b\]

가설의 H를 따서 사용하기도 합니다.

\[H(x)= Wx+b\]

여기서 x와 곱해지는 W는 가중치(weight)를 의미하고, b는 편향(bias)를 의미합니다. 가중치 W는 기울기를 의미하고 b는 y절편을 의미하겠죠? 배운거 어디 안갑니다~

Cost Function

앞으로 딥러닝을 학습하면서 비용 함수(cost function) = 손실 함수(loss function) = 오차함수(error function) = 목적 함수(objective fuction)

비용함수에 대한 이해를 위한 예제입니다. 이 비용함수는 선형대수학의 최소제곱해와 같습니다. (이하 최소제곱직선) 이 예제를 분석해보면 왜 선형대수학에서 최소’제곱’직선 이라고 불리는지 알 수 있습니다.

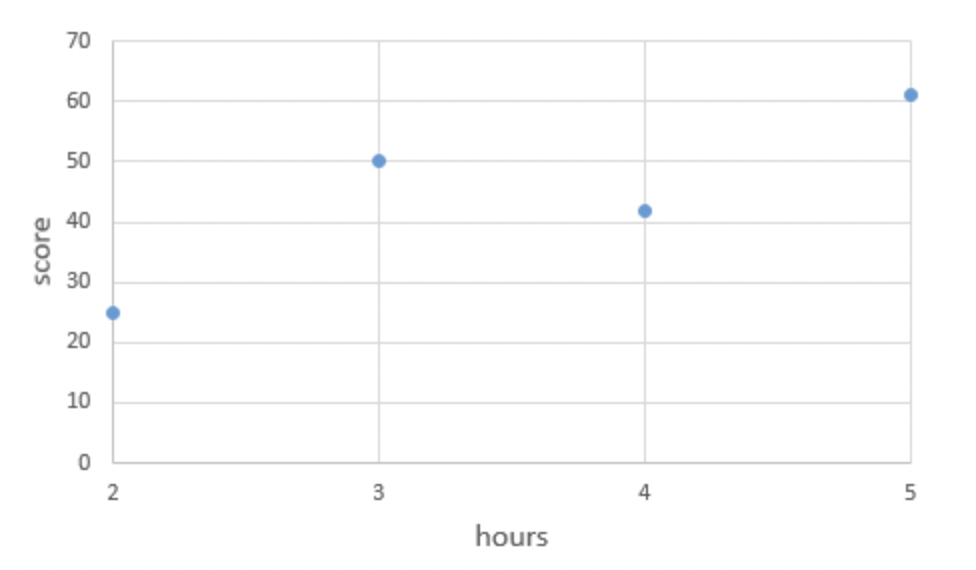
그래프상에 한직선으로 표현할 수 없는 네개의 점이 있다고 합시다.

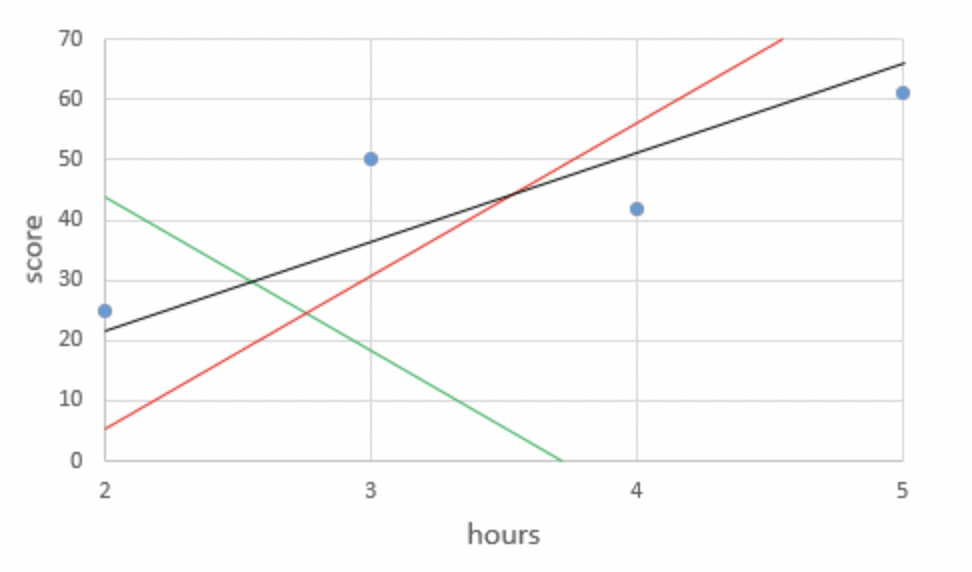
최대한 4개의 점과 가까운 직선을 찾아주세요 하는 문제인건데, 사람에따라 빨간선이 혹은 검정선이 제일 가깝다고 생각 할 수 있지만 이를 수학적으로 정확하게 나타내야하므로 필요한것이 최소제곱해이다.

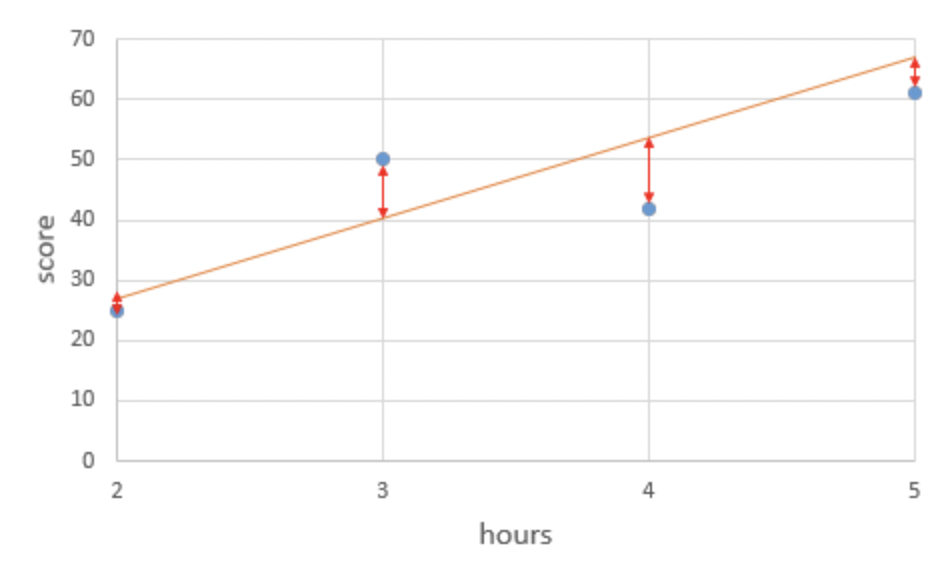
주황색 직선에서 실제값(점) 과 예측값(주황색선) 의 빨간막대기의 길이만큼을 오차라고 할 때,

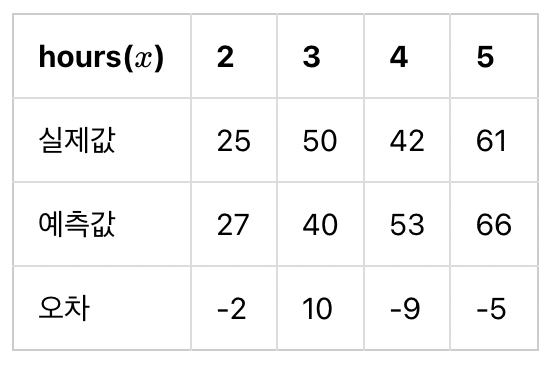
이렇게 오차가 음수인 경우도 생길 수 있는데 만약 오차가 두개가 있었는데 하나는 -10 다른 하나는 +10이라하면 그냥 오차끼리 더해버리면 오차가 0이 되어버려서, 해석하는 입장에서는 완벽한 해를 구했다고 생각할 수 있다.

그래서 우리는 오차들을 제곱해서 더한 뒤

\[\sum_{i=1}^{n} \left[y^{(i)} - H(x^{(i)})\right]^2 = (-2)^{2} + 10^{2} + (-9)^{2} + (-5)^{2} = 210\]

이를 데이터의 개수인 n으로 나누면

\[\frac{1}{n} \sum_{i=1}^{n} \left[y^{(i)} - H(x^{(i)})\right]^2 = 210 / 4 = 52.5\]

이를 평균 제곱 오차(Mean Squared Error, MSE)라고 합니다. 이러한 평균 제곱 오차를 이용해서 가장 훈련 데이터를 잘 반영한 W 와 b를 찾아낼 수 있습니다. cost function을 재정의하면

\[cost(W, b) = \frac{1}{n} \sum_{i=1}^{n} \left[y^{(i)} - H(x^{(i)})\right]^2\]

Optimizer - 경사 하강법(Gradient descent)

앞서 말한 cost fuction을 최소화하는 W 와 b를 찾아야하는데 이 때 사용되는 것이 Optimizer 알고리즘입니다. 가장 기본적인 옵티마이저 알고리즘은 경사 하강법입니다.

이름에서 알 수 있는 힌트는 gradient인데, gradient란, 다른말로 경도벡터라고도 불립니다. 이는 쉽게말하면 어떠한 곡선의 접선의 기울기를 뜻한다고 보면 되겠습니다.

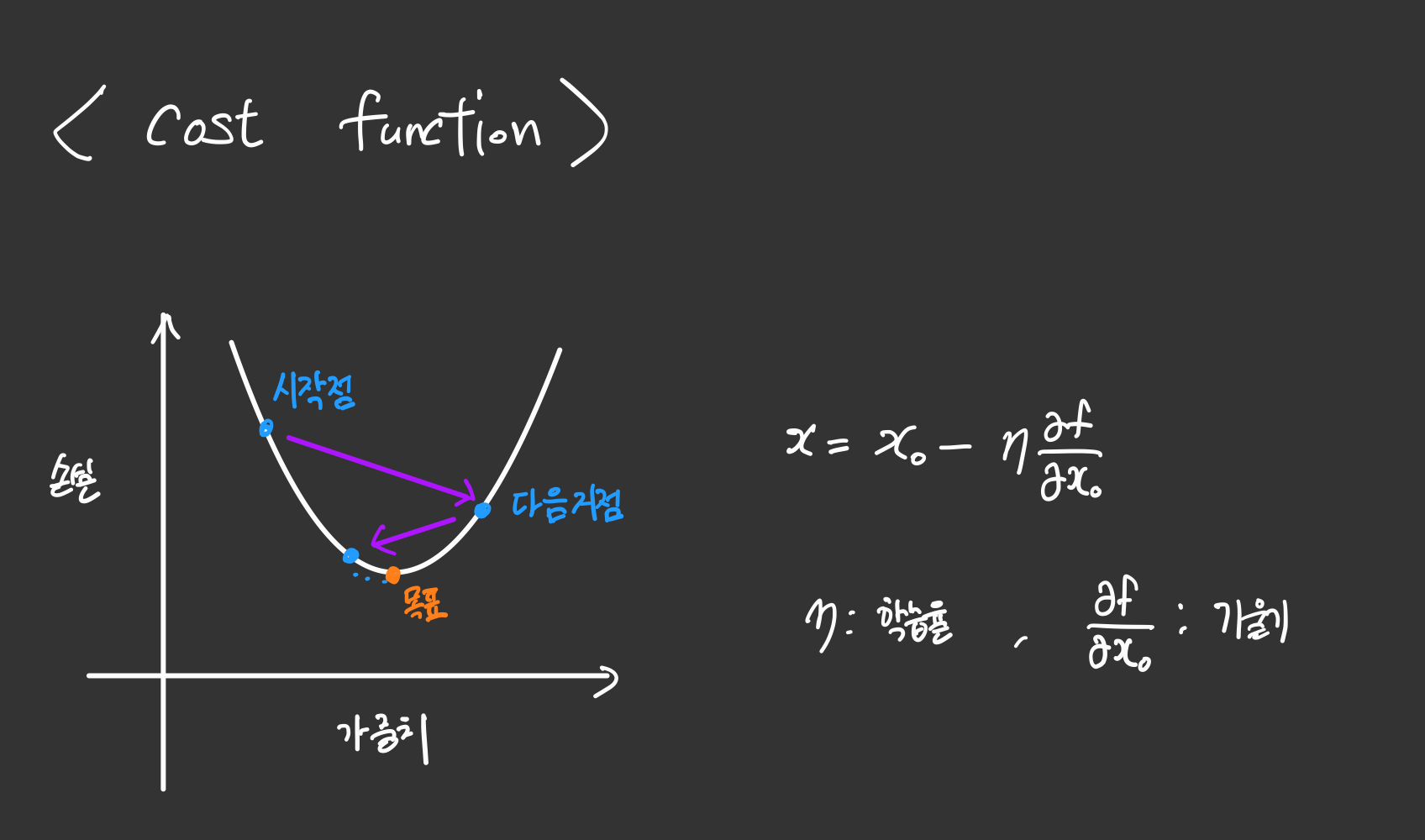
Cost function이 cos 함수인데 초기 W,b값에 따라서 시작점이 정해집니다.

그 시작점의 기울기를 구해서 음수이면 오른쪽으로 양수이면 왼쪽으로 이동해서 마치 이차함수의 꼭지점으로 향해가는 모습을 상상해보면 최적으로 향해간다고 볼 수 있습니다.

(cost 함수의 최소값 = 꼭지점 = 미분계수가 0이되는 순간)

학습률은 너무 크면 발산하고 너무 작으면 계산의 속도가 너무 느려지기 때문에 적당한 값을 찾는 것이 중요합니다.

• 가설, 비용 함수, 옵티마이저는 머신 러닝 분야에서 사용되는 포괄적 개념입니다. 풀고자하는 각 문제에 따라 가설, 비용 함수, 옵티마이저는 전부 다를 수 있으며 선형 회귀에 가장 적합한 비용 함수는 평균 제곱 오차, 옵티마이저는 경사 하강법입니다. (wikidocks)
  
  

파이토치로 구현하기

• 파이토치 초기설정

  import torch
  import torch.nn as nn
  import torch.nn.functional as F
  import torch.optim as optim
  

  
  

• 초기 시드 값을 줍시다. 시드값에 따라 초기값이 달라집니다.

  torch.manual_seed(1)
  

  위에서 나왔던 입출력값입니다. 예제랑은 살짝 다릅니다.

  x_train = torch.FloatTensor([[1], [2], [3]])
  y_train = torch.FloatTensor([[2], [5], [9]])
  

  # 가중치 W, 편향 b를 0으로 초기화하고 학습을 통해 값이 변경되는 변수임을 명시함.
  W = torch.zeros(1, requires_grad=True) 
  b = torch.zeros(1, requires_grad=True)
  

  가중치와 편향을 0으로 초기화하는 이유는 초기가설이 0을 예측하게 하기 위함입니다.

requires_grad = True 라는 말은 학습을 통해 계속 바뀌는 변수라는 의미입니다.

• 이제 가설을 설정해줍니다.

  hypothesis = x_train * W + b
  

  
  

• 비용함수를 선언해줍니다. 앞서 배운 mean 함수를 활용하면

\[cost(W, b) = \frac{1}{n} \sum_{i=1}^{n} \left[y^{(i)} - H(x^{(i)})\right]^2\]

cost = torch.mean((hypothesis - y_train) ** 2) 

optimizer = optim.SGD([W, b], lr=0.01)

lr은 학습률을 말합니다.

optimizer.zero_grad 가 필요한 이유는 파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시키는 특징이 있습니다.

한번 예를 들어볼까요?

import torch
w = torch.tensor(2.0, requires_grad=True)

nb_epochs = 20
for epoch in range(nb_epochs + 1):

  z = 2*w

  z.backward()
  print('수식을 w로 미분한 값 : {}'.format(w.grad))

결과값

수식을 w로 미분한 값 : 2.0
수식을 w로 미분한 값 : 4.0
수식을 w로 미분한 값 : 6.0
수식을 w로 미분한 값 : 8.0
수식을 w로 미분한 값 : 10.0
수식을 w로 미분한 값 : 12.0
수식을 w로 미분한 값 : 14.0
수식을 w로 미분한 값 : 16.0
수식을 w로 미분한 값 : 18.0
수식을 w로 미분한 값 : 20.0
수식을 w로 미분한 값 : 22.0
수식을 w로 미분한 값 : 24.0
수식을 w로 미분한 값 : 26.0
수식을 w로 미분한 값 : 28.0
수식을 w로 미분한 값 : 30.0
수식을 w로 미분한 값 : 32.0
수식을 w로 미분한 값 : 34.0
수식을 w로 미분한 값 : 36.0
수식을 w로 미분한 값 : 38.0
수식을 w로 미분한 값 : 40.0
수식을 w로 미분한 값 : 42.0

계속해서 미분값 2가 누적되기 때문에 초기화를 해주어야 하는 것입니다.

# gradient를 0으로 초기화
optimizer.zero_grad() 
# 비용 함수를 미분하여 gradient 계산
cost.backward() 
# W와 b를 업데이트
optimizer.step() 

optimizer.zero_grad()를 실행하므로서 미분을 통해 얻은 기울기를 0으로 초기화합니다.

기울기를 초기화해야만 새로운 가중치 편향에 대해서 새로운 기울기를 구할 수 있습니다.

그 다음 cost.backward() 함수를 호출하면 가중치 W와 편향 b에 대한 기울기가 계산됩니다.

그 다음 경사 하강법 최적화 함수 opimizer의 .step() 함수를 호출하여 인수로 들어갔던 W와 b에서 리턴되는 변수들의 기울기에 학습률(learining rate) 0.01을 곱하여 빼줌으로서 업데이트합니다.

이제 전체 코드를 한번에 보면

# 데이터
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[5],[9]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W,b], lr=0.01)

n_epochs = 3000 #원하는 만큼 확률적 경사 강하법 실행 총 3000번 실행
for epoch in range(n_epochs + 1):
    
    #H(x) 계산
    hyphothesis = x_train * W + b
    
    #cost 손실함수 계산
    cost = torch.mean((hyphothesis - y_train) ** 2)
    
    #cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    #100번마다 로그 출력
    if epoch % 100 == 0 :
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
            epoch, n_epochs, W.item(), b.item(), cost.item()
        ))

Epoch    0/3000 W: 0.260, b: 0.107 Cost: 36.666668
Epoch  100/3000 W: 2.573, b: 0.440 Cost: 0.695327
Epoch  200/3000 W: 2.771, b: -0.011 Cost: 0.450896
Epoch  300/3000 W: 2.927, b: -0.365 Cost: 0.299852
Epoch  400/3000 W: 3.050, b: -0.643 Cost: 0.206516
Epoch  500/3000 W: 3.146, b: -0.862 Cost: 0.148840
Epoch  600/3000 W: 3.222, b: -1.034 Cost: 0.113199
Epoch  700/3000 W: 3.281, b: -1.170 Cost: 0.091176
Epoch  800/3000 W: 3.328, b: -1.276 Cost: 0.077567
Epoch  900/3000 W: 3.365, b: -1.359 Cost: 0.069157
Epoch 1000/3000 W: 3.394, b: -1.425 Cost: 0.063960
Epoch 1100/3000 W: 3.416, b: -1.477 Cost: 0.060749
Epoch 1200/3000 W: 3.434, b: -1.517 Cost: 0.058765
Epoch 1300/3000 W: 3.448, b: -1.549 Cost: 0.057539
Epoch 1400/3000 W: 3.459, b: -1.574 Cost: 0.056781
Epoch 1500/3000 W: 3.468, b: -1.594 Cost: 0.056313
Epoch 1600/3000 W: 3.475, b: -1.610 Cost: 0.056023
Epoch 1700/3000 W: 3.480, b: -1.622 Cost: 0.055845
Epoch 1800/3000 W: 3.485, b: -1.631 Cost: 0.055734
Epoch 1900/3000 W: 3.488, b: -1.639 Cost: 0.055666
Epoch 2000/3000 W: 3.490, b: -1.645 Cost: 0.055624
Epoch 2100/3000 W: 3.492, b: -1.650 Cost: 0.055598
Epoch 2200/3000 W: 3.494, b: -1.653 Cost: 0.055582
Epoch 2300/3000 W: 3.495, b: -1.656 Cost: 0.055572
Epoch 2400/3000 W: 3.496, b: -1.658 Cost: 0.055566
Epoch 2500/3000 W: 3.497, b: -1.660 Cost: 0.055562
Epoch 2600/3000 W: 3.498, b: -1.662 Cost: 0.055559
Epoch 2700/3000 W: 3.498, b: -1.663 Cost: 0.055558
Epoch 2800/3000 W: 3.499, b: -1.663 Cost: 0.055557
Epoch 2900/3000 W: 3.499, b: -1.664 Cost: 0.055556
Epoch 3000/3000 W: 3.499, b: -1.665 Cost: 0.055556

에포크(Epoch)는 전체 훈련 데이터가 학습에 한 번 사용된 주기를 말합니다. 이번 실습의 경우 3,000번을 수행했습니다.

이렇게 W는 약 3.5, b는 -1.665에 가까워지는 것을 볼 수 있습니다. 이를 기준으로 처음에 입출력값과 최소제곱직선을 비교해보면

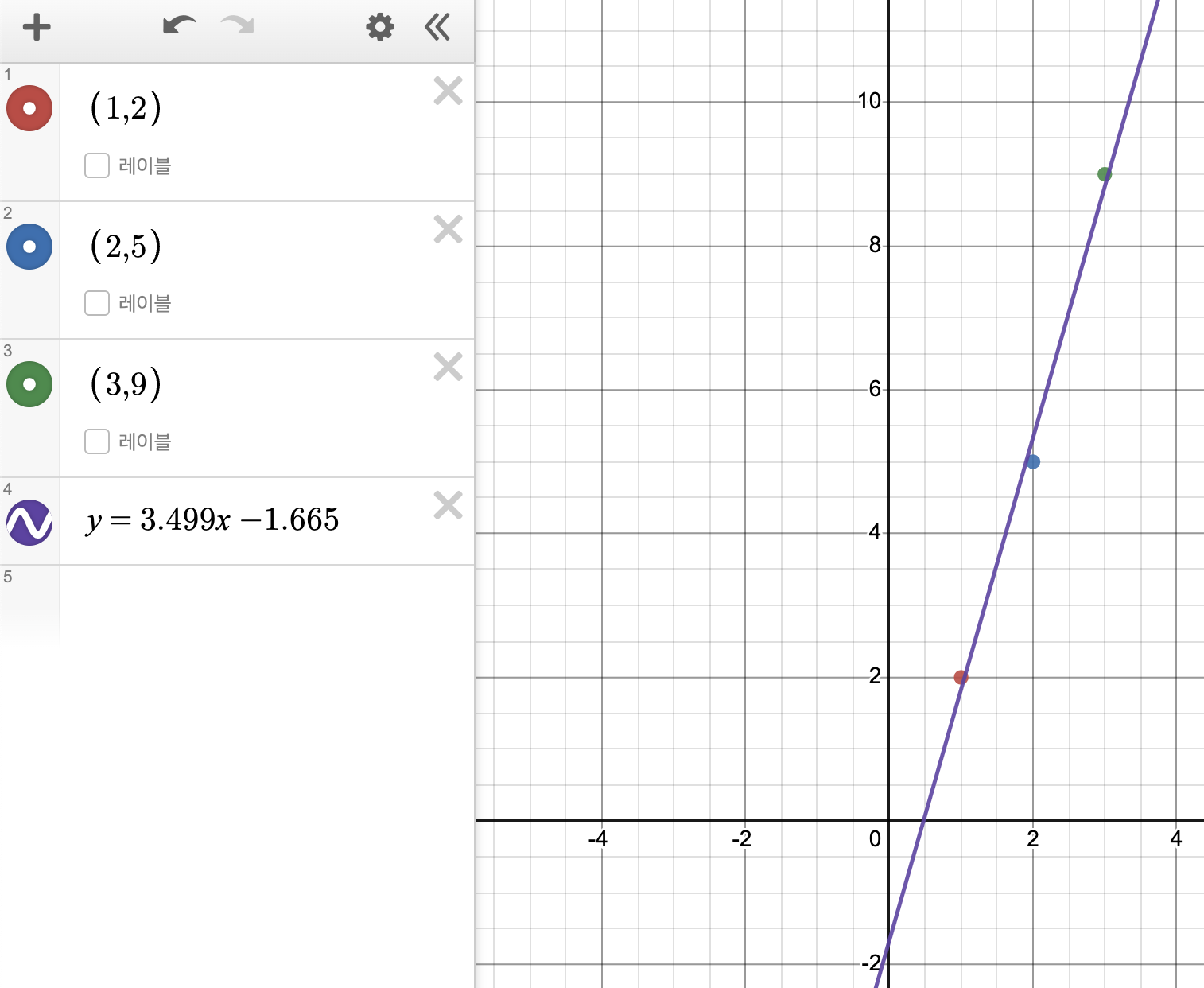
완전 근사한 직선이라는 것을 직관적으로 볼 수 있습니다.

[추가내용.7.28]

---

SGD, 경사하강법

SGD는 Stochastic Gradient Descent의 약어로 배치 크기가 1인 경사 강하법입니다.

(확률적 경사하강법) 은 배치크기가 1인 경사하강법 알고리즘입니다. 데이터셋에서 무작위로 뽑은 하나의 예를 가지고 계산하는 방식.

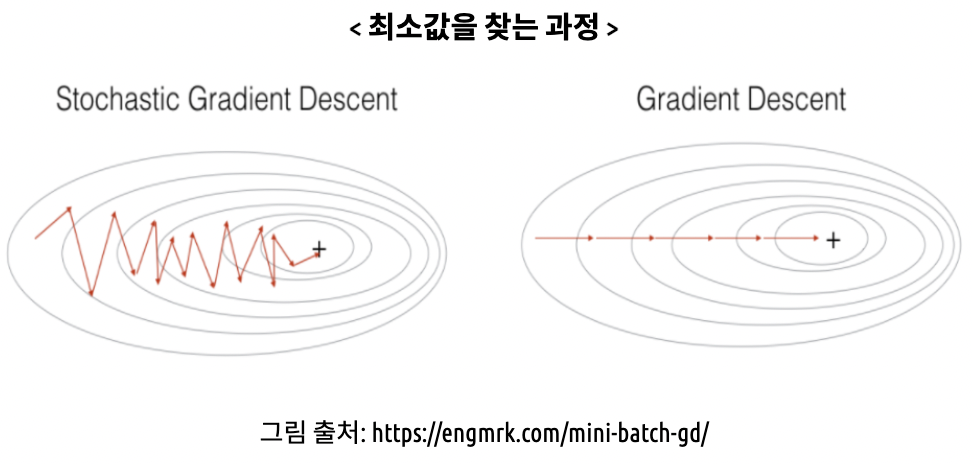
Batch(배치)

경사하강법에서 배치란 단일 반복에서 기울기를 계산하는데 사용하는 data의 총 개수입니다.

Gradient Descent에서 배치는 전체 데이터 셋이라고 가정합니다.

대규모작업에서 데이터셋에 수십억, 수천억개의 예시가 포함되는 경우가 많습니다. 그럴 때마다 단일 반복으로 계산을하게되면 너무 오랜시간이 걸릴 수 있습니다.

그러한 대규모의 데이터에는 그만큼 중복이 되는 데이터가 있을 가능성이 높기 때문에, 데이터에서 무작위로 선택하면(노이즈는 있겠지만) 훨씬 빠르게 값들을 얻을 수가 있게됩니다.

‘확률적 경사하강법(SGD)’은 이러한 개념을 조금더 확장한 방법입니다. 반복당 하나의 예(배치 크기가 1)만을 사용합니다.

‘확률적(Stochastic)이라는 용어는 각 배치를 포함하는 하나의 예가 무작위로 선택된다는 것을 의미합니다.

• SGD의 단점

  반복이 충분하면 효과는있지만, 노이즈가 심하다. 확률적 경사강하법의 여러 변형함수의 최저점을 찾을 확률은 높지만, 항상 보장되지는 않습니다
  

• 이러한 단점을 극복하기위해 나타난 것이 미니 배치 SGD 입니다.

  미니 배치는 일반적으로 무작위로 선택한 10개에서 1000개 사이의 예로 구성됩니다. 이 내용은 추후 ‘딥러닝 공부 4일차’에서 배웁니다. —

참고문헌 : wikidocs, tistory

---

끝!