Lec 04-1: Multivariabel Linear Regression
딥러닝 공부 4일차
Multivariable Linear Regression
앞서 배운 Linear Regresstion 은 x가 1개인 선형회귀였습니다. 하지만 현실은 어떠한 결과를 내는데 원인이 한가지만 있는경우는 드물죠 만약 x가 여러개면 어떻게될까요?
x가 여러개인 선형회귀를 다항 선형회귀라고 합니다. 퍼셉트론 관점으로는 다중퍼셉트론이라고 할 수 있겠네요.
- 다항 선형 회귀(Multivariabel Linear Regression)
- 가설 함수(Hypothesis Function)
- 평균 제곱 오차(Mean Squared Error)
- 경사하강법(Gradient descent)
Data Definition
다음과 같은 학슴데이터가 있다고 가정해보겠습니다. 앞서 배운 단순 선형회귀와는 달리 독립변수 x가 3개입니다.
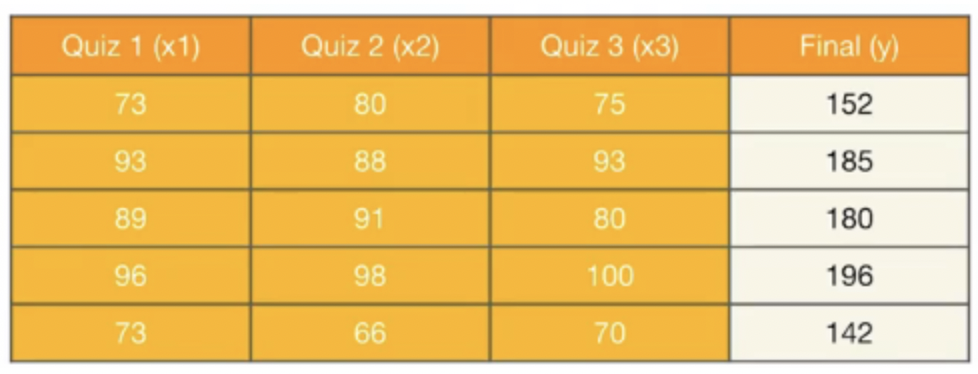
가설의 식은 아래와 같게 변합니다.
\(H(x) = w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3} + b\)
파이토치로 구현하기
이러한 다중선형회귀를 파이토치로 구현한다면 다음과 같습니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x1_train = torch.FloatTensor([[73], [93], [89], [96], [73]])
x2_train = torch.FloatTensor([[80], [88], [91], [98], [66]])
x3_train = torch.FloatTensor([[75], [93], [90], [100], [70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
w1 = torch.zeros(1, requires_grad=True)
w2 = torch.zeros(1, requires_grad=True)
w3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([w1, w2, w3, b], lr=1e-5)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
hypothesis = x1_train * w1 + x2_train * w2 + x3_train * w3 + b
cost = torch.mean((hypothesis - y_train) ** 2)
optimizer.zero_grad()
cost.backward()
optimizer.step()
if epoch % 100 == 0:
print('Epoch {:4d}/{} w1: {:.3f} w2: {:.3f} w3: {:.3f} b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, w1.item(), w2.item(), w3.item(), b.item(), cost.item()
))
코드를 실행한 결과값은 다음과 같습니다.
Epoch 0/1000 w1: 0.294 w2: 0.294 w3: 0.297 b: 0.003 Cost: 29661.800781
Epoch 100/1000 w1: 0.674 w2: 0.661 w3: 0.676 b: 0.008 Cost: 1.563634
Epoch 200/1000 w1: 0.679 w2: 0.655 w3: 0.677 b: 0.008 Cost: 1.497607
Epoch 300/1000 w1: 0.684 w2: 0.649 w3: 0.677 b: 0.008 Cost: 1.435026
Epoch 400/1000 w1: 0.689 w2: 0.643 w3: 0.678 b: 0.008 Cost: 1.375730
Epoch 500/1000 w1: 0.694 w2: 0.638 w3: 0.678 b: 0.009 Cost: 1.319511
Epoch 600/1000 w1: 0.699 w2: 0.633 w3: 0.679 b: 0.009 Cost: 1.266222
Epoch 700/1000 w1: 0.704 w2: 0.627 w3: 0.679 b: 0.009 Cost: 1.215696
Epoch 800/1000 w1: 0.709 w2: 0.622 w3: 0.679 b: 0.009 Cost: 1.167818
Epoch 900/1000 w1: 0.713 w2: 0.617 w3: 0.680 b: 0.009 Cost: 1.122429
Epoch 1000/1000 w1: 0.718 w2: 0.613 w3: 0.680 b: 0.009 Cost: 1.079378
W1은 약 0.71, W2는 약 0.61, W3는 약 0.68 그리고 b는 0.009 에 가까워지는 것을 볼 수 있습니다.
cost 값은 초기값 약 3만에서 1로 찾아가는 것을 볼 수 있습니다.
선형대수학의 중요성
현실에서 사용되는 딥러닝은 수많은 학습데이터가 존재합니다. 만약에 x의 개수 천개, 만개로 늘어난다면 그에 상응하는 가중치값도 천개, 만개로 늘어날 것이고 그렇다면 위의 파이토치로 구현한 것 처럼 연산을해준다면, 코드가 무한하게 늘어날 것입니다.
이러한 문제점을 벡터와 행렬연산으로 바꿔준다면 아주 쉽게 해결됩니다.
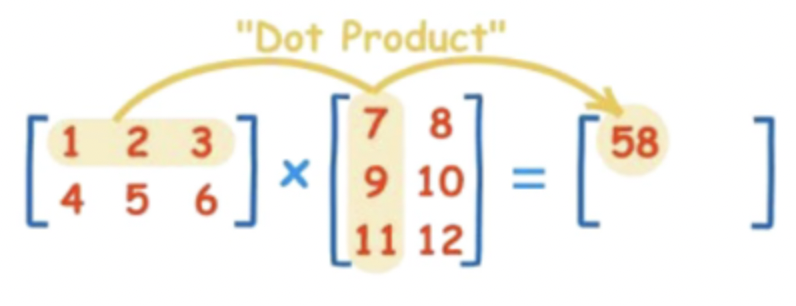
행렬과 행렬간의 내적을 통해 연산을 간소화시킬 수 있는데요,
\[H(X) = w_{1}x_{1} + w_{2}x_{2} + w_{3}x_{3}\]위와 같은 식을 행렬의 곱으로 표현하면
\[\left( \begin{array}{c} x_{1}\ x_{2}\ x_{3}\ \\ \end{array} \right) \left( \begin{array}{c} w_{1} \\ w_{2} \\ w_{3} \\ \end{array} \right) \ = \left( \begin{array}{c} x_{1}w_{1}+ x_{2}w_{2}+ x_{3}w_{3}\ \\ \end{array} \right)\]처럼 간단하게 나타낼 수 있습니다. 또한 두 벡터를 각각 $X$ 와 $W$ 라고한다면 다음과 같이 더욱 간단하게도 표현할 수 있습니다.
\[H(X) = XW\]
아까위에서 보여드렸던 예제 표입니다. 이렇게 여러가지 변수들을 행렬의 곱으로 표현하면
\[\left( \begin{array}{c} x_{11}\ x_{12}\ x_{13}\ \\ x_{21}\ x_{22}\ x_{23}\ \\ x_{31}\ x_{32}\ x_{33}\ \\ x_{41}\ x_{42}\ x_{43}\ \\ x_{51}\ x_{52}\ x_{53}\ \\ \end{array} \right) \left( \begin{array}{c} w_{1} \\ w_{2} \\ w_{3} \\ \end{array} \right) \ = \left( \begin{array}{c} x_{11}w_{1}+ x_{12}w_{2}+ x_{13}w_{3}\ \\ x_{21}w_{1}+ x_{22}w_{2}+ x_{23}w_{3}\ \\ x_{31}w_{1}+ x_{32}w_{2}+ x_{33}w_{3}\ \\ x_{41}w_{1}+ x_{42}w_{2}+ x_{43}w_{3}\ \\ x_{51}w_{1}+ x_{52}w_{2}+ x_{53}w_{3}\ \\ \end{array} \right)\]처럼 표현할 수 있습니다.
행렬의연산을 파이토치로 구현하기
행렬연산을 고려할 것이기 때문에 훈련데이터도 행렬로 선언해주어야합니다.
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 80],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
가중치와 편향을 설정해줍니다
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
여기서 왜 W가 (3x1) 이냐면 x_train이 (5x3) 행렬이기 때문에 행렬의 곱을 하기위한 조건으로 W의 행은 3행이 되고 출력값에 전달하는 값은 하나의 스칼라값이 되어야하기 때문에 1열을 가지게 되는 것입니다.
hypothesis = x_train.matmul(W) + b
이 한줄이 강력한 한방입니다. 위의 일반적인 파이토치로 구현하는 연산보다 훨씬 간편해진 것을 알 수 있습니다. 이후에 입력 출력값이 어떻게 변하든 그냥 그 부분만 수정해주면 된다는 점이 아주 맘에드네요.
nn.Module로 구현하는 선형회귀
이전까지는 가설, 비용함수를 직접 정의해서 선형회귀를 구현했다면, 이번에는 파이토치에서 기본으로 제공해주는 함수를 통해서 더 쉽게 구현해보려고 합니다.
예를 들어 파이토치에서는 선형 회귀 모델이 nn.Linear()라는 함수로, 또 평균 제곱오차가 nn.functional.mse_loss()라는 함수로 세팅되어져있습니다.
import torch.nn as nn
model = nn.Linear(input_dim, output_dim
import torch.nn.functional as F
cost = F.mse_loss(prediction, y_train)
여기서 nn과 nn.functional 의 차이점은 클래스냐 함수냐 차이일뿐 두 방식 다 같은 결과를 제공해주기 때문에 편한 것, 더 취향에 끌리는 것을 사용하면 된다
torch.nn 은 클래스이고, torch.nn.funtional은 함수입니다.
torch.nn으로 구현한 클래스의 경우에는 attribute를 활용해 state를 저장하고 활용할 수 있고 torch.nn.functional로 구현한 함수의 경우에는 인스턴스화 시킬 필요 없이 사용이 가능합니다.
”????”
파이썬 (클래스, 오브젝트, 상속)
위의 말이 무슨말인지 모르겠다면 파이썬을 조금더 공부할 필요가 있다. 필자가 그랬습니다 ^^

클래스는 빵틀이라고 보면 편합니다.
오브젝트(객체,인스턴스,instance)는 클래스 즉, 빵틀로 찍어낸 빵이라고 생각하면 이해하기 쉽습니다. 또한 attribute는 객체의 특징입니다.
여기 필자가 공부하다가 발견한 Class 와 Instance 의 좋은예가 있어서 소개해드립니다.
#삼각김밥 클래스
class Samgak:
def __init__(self):
self.source = '기본 소스'
self.kim = '광O 김'
self.bab = '쌀밥'
self.food = ''
def set_source(self, source_name):
self.source = source_name
def change_kim(self, kim_name):
self.kim = kim_name
def change_bab(self, bab_name):
self.bab = bab_name
def set_food(self, food_name):
self.food = food_name
def print(self):
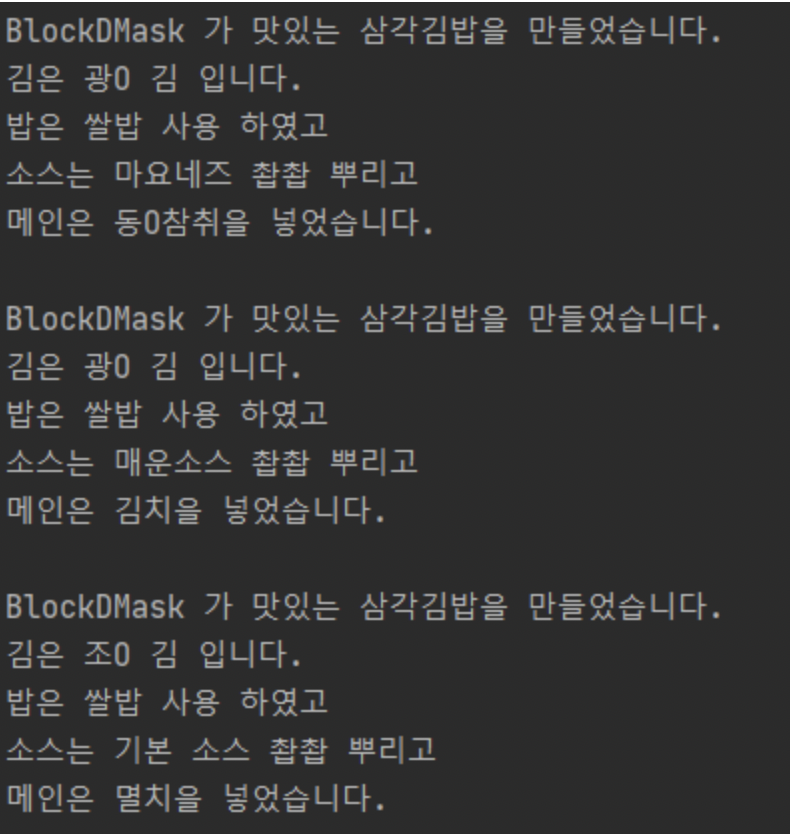
s1 = 'BlockDMask 가 맛있는 삼각김밥을 만들었습니다.\n'
s1 += f'김은 {self.kim} 입니다.\n'
s1 += f'밥은 {self.bab} 사용 하였고\n'
s1 += f'소스는 {self.source} 촵촵 뿌리고\n'
s1 += f'메인은 {self.food}을 넣었습니다.\n'
print(s1)
# 참치 삼각 김밥
chamchi = Samgak()
chamchi.set_food('동O참취')
chamchi.set_source('마요네즈')
chamchi.print()
# 매운 김치 삼각 김밥
kimchi = Samgak()
kimchi.set_food('김치')
kimchi.set_source('매운소스')
kimchi.print()
# 멸치 삼각 김밥
mulchi = Samgak()
mulchi.change_kim('조O 김')
mulchi.set_food('멸치')
mulchi.print()
결과값
위 예제에서 클래스에 대해서 알아보았으니 이제 상속(inheritance)에 대해서 알아봅시다.
어떠한 공통적인 특징은 지니지만, 세부적인 특징은 다르게하고싶을 때, 상속을 많이 사용하게됩니다.
가령 예를들어 경찰관, 프로그래머 등.. 여러 직업을 가진사람들은 사람이라는 공통적인 특징은 공유하지만 직업적 특징은 다르므로 아래와 같이 코드를 작성해 볼 수 있습니다.
# 사람이라는 기본적인 공통구조 = 클래스
class Person:
def __init__(self, name, age):
self.name = name
self.age = age
def say_hello(self, to_name):
print("안녕! " + to_name + " 나는 " + self.name + "\n")
def introduce(self):
print("내 이름은 " + self.name + " 그리고 나는 " + str(self.age) + "살이야\n")
# 경찰은 사람의 특징도 갖고 추가로 경찰관의 특징을 갖죠!
class Police(Person):
def arrest(self, to_arrest):
print("넌 체포됐다, " + to_arrest + "\n")
# 프로그래머는 사람의 특징을 가지면서 추가로 프로그래머의 특징을 갖죠!
class Programmer (Person):
def program(self, to_program):
print("다음엔 뭘 만들지? 아 이걸 만들어야겠다: " + to_program + "\n")
jiwon = Person("지원", 25)
jihye = Police("지혜", 26)
yuchul = Programmer("유철", 25)
jihye.introduce()
jihye.say_hello("유철")
jihye.arrest("유철")
yuchul.introduce()
yuchul.say_hello("지혜")
yuchul.program("pitching 분석프로그램")
결과를 출력해보면 아래와 같습니다. 부디 이해가 가길 바랍니다.
내 이름은 지혜 그리고 나는 26살이야
안녕! 유철 나는 지혜
넌 체포됐다, 유철
내 이름은 유철 그리고 나는 25살이야
안녕! 지혜 나는 유철
다음엔 뭘 만들지? 아 이걸 만들어야겠다: 딥러닝 깃허브 블로그
이제 파이썬에 클래스, 오브젝트, 상속에대해서 얼추 알았으니 마저 이어서 공부해봅시다.
클래스로 파이토치 모델 구현하기
모델을 클래스로 구현하기
앞서 구현한 코드와 다른점은 오로지 클래스로만 구현할 것이라는 점입니다.
# 모델을 선언 및 초기화. 단순 선형 회귀이므로 input_dim=1, output_dim=1.
model = nn.Linear(1,1)
class LinearRegressionModel(nn.Module): # torch.nn.Module을 상속받는 파이썬 클래스
def __init__(self): #
super().__init__()
self.linear = nn.Linear(1, 1) # 단순 선형 회귀이므로 input_dim=1, output_dim=1.
def forward(self, x):
return self.linear(x)
model = LinearRegressionModel()
클래스(class) 형태의 모델은 nn.Module 을 상속받습니다. 그리고 init()에서 모델의 구조와 동작을 정의하는 생성자를 정의합니다.
이는 파이썬에서 객체가 갖는 속성값을 초기화하는 역할로, 객체가 생성될 때 자동으로 호출됩니다.
super() 함수를 부르면 여기서 만든 클래스는 nn.Module 클래스의 속성들을 가지고 초기화 됩니다.
foward() 함수는 모델이 학습데이터를 입력받아서 forward 연산을 진행시키는 함수입니다. forward() 함수는 model 객체를 데이터와 함께 호출하면 자동으로 실행이됩니다.
예를 들어 model이란 이름의 객체를 생성 후, model(입력 데이터)와 같은 형식으로 객체를 호출하면 자동으로 forward 연산이 수행됩니다.
이제 다중선형회귀 모델을 구현해보면
# 모델을 선언 및 초기화. 다중 선형 회귀이므로 input_dim=3, output_dim=1.
model = nn.Linear(3,1)
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1) # 다중 선형 회귀이므로 input_dim=3, output_dim=1.
def forward(self, x):
return self.linear(x)
model = MultivariateLinearRegressionModel()
클래스의 이름과 linear 옆의 사이즈만 달라진 것을 확인할 수 있습니다.
단순선형회귀 Full code.
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
class LinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
model = LinearRegressionModel()
# optimizer 설정. 경사 하강법 SGD를 사용하고 learning rate를 의미하는 lr은 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 전체 훈련 데이터에 대해 경사 하강법을 2,000회 반복
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward() # backward 연산
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
다중선형회귀 Full code.
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(1)
# 데이터
x_train = torch.FloatTensor([[73, 80, 75],
[93, 88, 93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1) # 다중 선형 회귀이므로 input_dim=3, output_dim=1.
def forward(self, x):
return self.linear(x)
model = MultivariateLinearRegressionModel()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 2000
for epoch in range(nb_epochs+1):
# H(x) 계산
prediction = model(x_train)
# model(x_train)은 model.forward(x_train)와 동일함.
# cost 계산
cost = F.mse_loss(prediction, y_train) # <== 파이토치에서 제공하는 평균 제곱 오차 함수
# cost로 H(x) 개선하는 부분
# gradient를 0으로 초기화
optimizer.zero_grad()
# 비용 함수를 미분하여 gradient 계산
cost.backward()
# W와 b를 업데이트
optimizer.step()
if epoch % 100 == 0:
# 100번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))

댓글남기기