Lec 06: Softmax Classification

딥러닝 공부 7일차

Softmax Classification

• Multinomial classification
  
  

원활한 이해를 위한 사전 지식들

One-hot encoding(원-핫 인코딩)

이전 글 까지는 Binary classificaiton, 즉 이분법적으로만 분류하는 것에 대해서 배웠습니다.

하지만 항상 이분법적으로만 생각할 수는 없죠, 이제는 여러가지를 고려하는 Multinomial classification에 대해서 배워볼겁니다.

이제 선택해야하는 선택지의 개수가 늘어남에 따라 필요한 것이 바로 원-핫 인코딩입니다.

원-핫 인코딩은 각 선택지의 인덱스에 해당하는 원소에는 1을, 나머지에는 0의 값을 가지도록 하는 표현 방법입니다.

예를들어볼까요?

우리 광운대학교 로봇학부 학생을 분류하는 프로그램이 있다고 해봅시다.

양재민 학생은 0번 인덱스, 박상현 학생은 1번 인덱스, 정유철 학생은 2번 인덱스를 부여했다고 해보면, 각 선택지에 대해서 원-핫 인코딩 된 벡터는

양재민 = [1,0,0]
박상현 = [0,1,0]
정유철 = [0,0,1]

이와 같이 원-핫 인코딩으로 표현된 벡터를 One-hot vector(원-핫 벡터) 라고 합니다.

원-핫 벡터를 사용하는 이유

분류하는 대상간에 상관성이 있다면 말이 달라지겠지만, 상관성이 없이 분류만 필요한 상황이라고 생각해봅시다.

만약 원-핫 인코딩을 하지않고, 정수로 이루어진 벡터를 사용한다면 어떻게 될까요?

다시 예를들어 {양재민, 박상현, 정유철}이 {1,2,3}로 레이블이 된다면 손실 함수로 선형 회귀 챕터에서 배운 평균 제곱 오차, MSE를 통해 정수 인코딩이 어떤 오해를 불러일으키는지 확인할 수 있습니다.

$\hat{y}$은 예측값을 의미합니다.

\[Loss\ function = \frac{1}{n} \sum_i^{n} \left(y_{i} - \hat{y_{i}}\right)^2\]

실제 값이 상현(2)이일때, 예측값이 재민(1)이였다면 제곱 오차는 다음과 같습니다. $(2-1)^2=1$

실제 값이 정유철(3)일때, 예측값이 재민(1)이였다면 제곱 오차는 다음과 같습니다. $(3-1)^2=4$

즉, 재민이와 상현이 사이의 오차보다 재민이와 정유철과의 오차가 더 큽니다.

이는 기계에게 재민이가 정유철보다 상현이와 더 비슷하다라는 정보를 주는 것과 다름없습니다.

ㅋㅋㅋㅋ

이러면 안되겠지요~

이런 정수 인코딩이 3개가아니라 몇십개 몇백개라면, 그 제곱의 크기는 더욱더 커질 것입니다.

그래서 단순 분류를 해야하는 multinomial classification 에서는 각 클래스간의 제곱오차를 균등하게 만들어주기 위해서 원-핫 인코딩을 사용합니다.

만약 클래스간의 연관성이 있는 {10대,20대,30대,40대…} 혹은 {유년기,청소년기, 성년기, 노년기} 등.. 이런 부류에서는 정수 인코딩이 필요할 수 있습니다.

Discrete Probability Distribution(이산 확률 분포)

고등학교 때 수학시간에 배웠던 연속 확률 분포와 반대점에 있는 것이 이산 확률 분포입니다.

가장 대표적인 예로 주사위의 한 눈금이 나올 확률을 예로 들 수 있겠습니다.

주사위의 눈금 1이 나올 확률 = $\frac{1}{6}$ 주사위의 눈금 2이 나올 확률 = $\frac{1}{6}$ 주사위의 눈금 3이 나올 확률 = $\frac{1}{6}$ 주사위의 눈금 4이 나올 확률 = $\frac{1}{6}$ 주사위의 눈금 5이 나올 확률 = $\frac{1}{6}$ 주사위의 눈금 6이 나올 확률 = $\frac{1}{6}$

설마 방금 던진 주사위의 눈금이 2였다고 그 다음에 주사위를 던질 때 주사위가 2보단 다른 숫자가 나올 확률이 높다고 생각하시는 분들은 없겠죠??

이처럼 이산확률분포는 연속적인 그래프가 아닌

사진출처

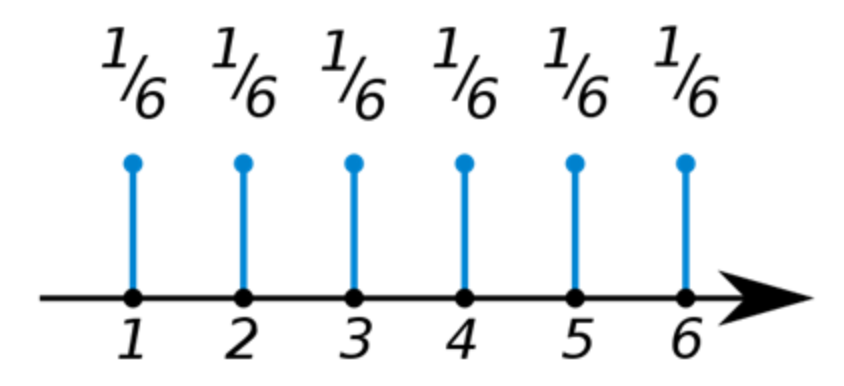
이런식으로 불연속적인 함수를 보이는 것이 특징이고, 모든 확률의 합은 1인 특징을 갖고 있습니다.

Multinomial Classification

사실 다항 분류에서도 로지스틱회귀를 응용하여 분류할 수 있습니다.

중간고사	기말고사	등급
90	65	A
90	50	A
39	40	B
25	49	B
10	15	C

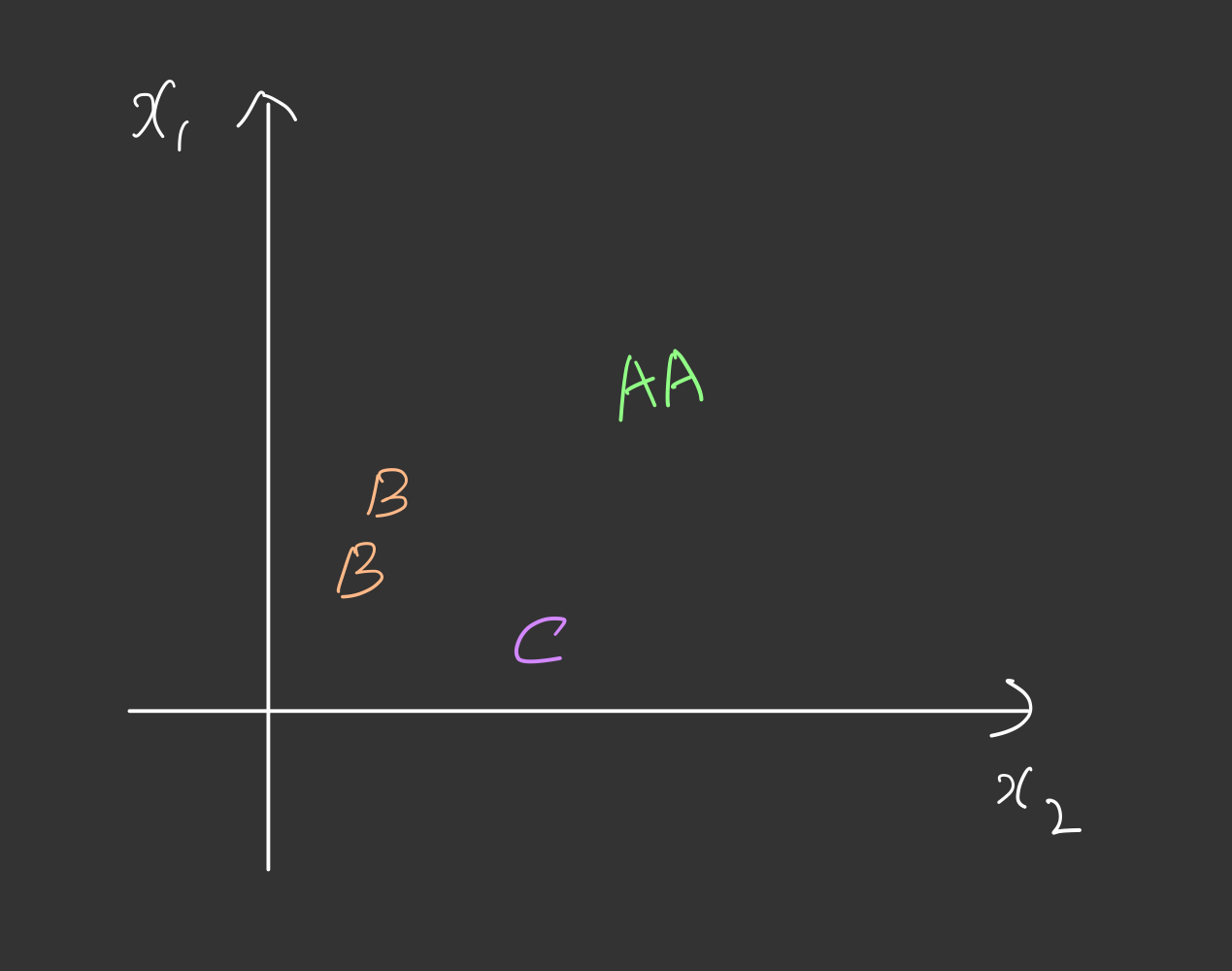
다음과 같이 중간고사와 기말고사 두개의 변수로 학생의 등급을 매기는 교수님이 있다고 해봅시다.

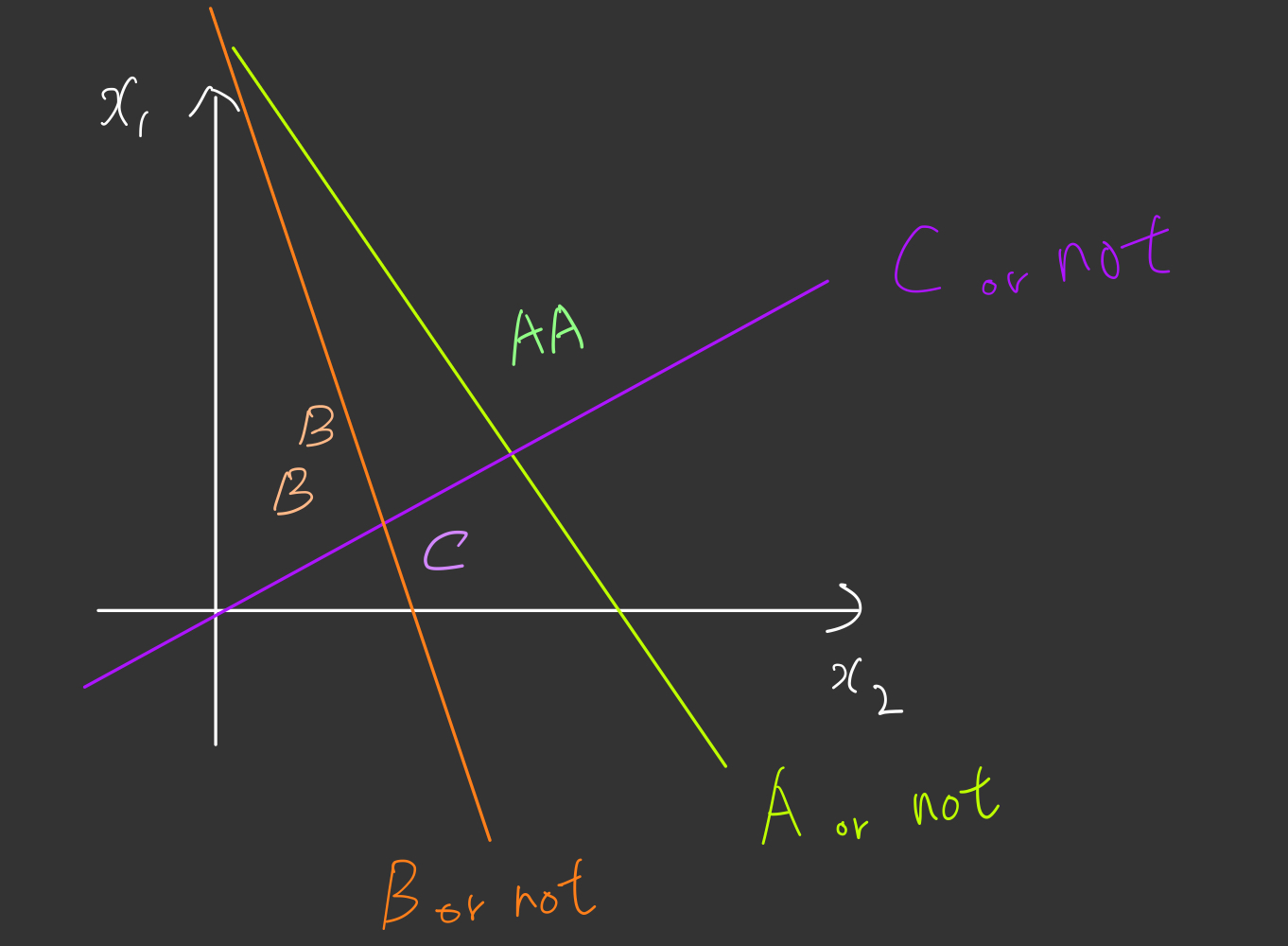
A그룹과 B그룹 그리고 C그룹을 어떻게 하면 선형회귀를 응용하여 분류할 수 있을까요??

정답은 위 그림과 같이 세가지 선으로써, A인지 아닌지, B인지 아닌지, C인지 아닌지에 해당하는 세가지 선의 조합으로 구별해낼 수 있습니다.

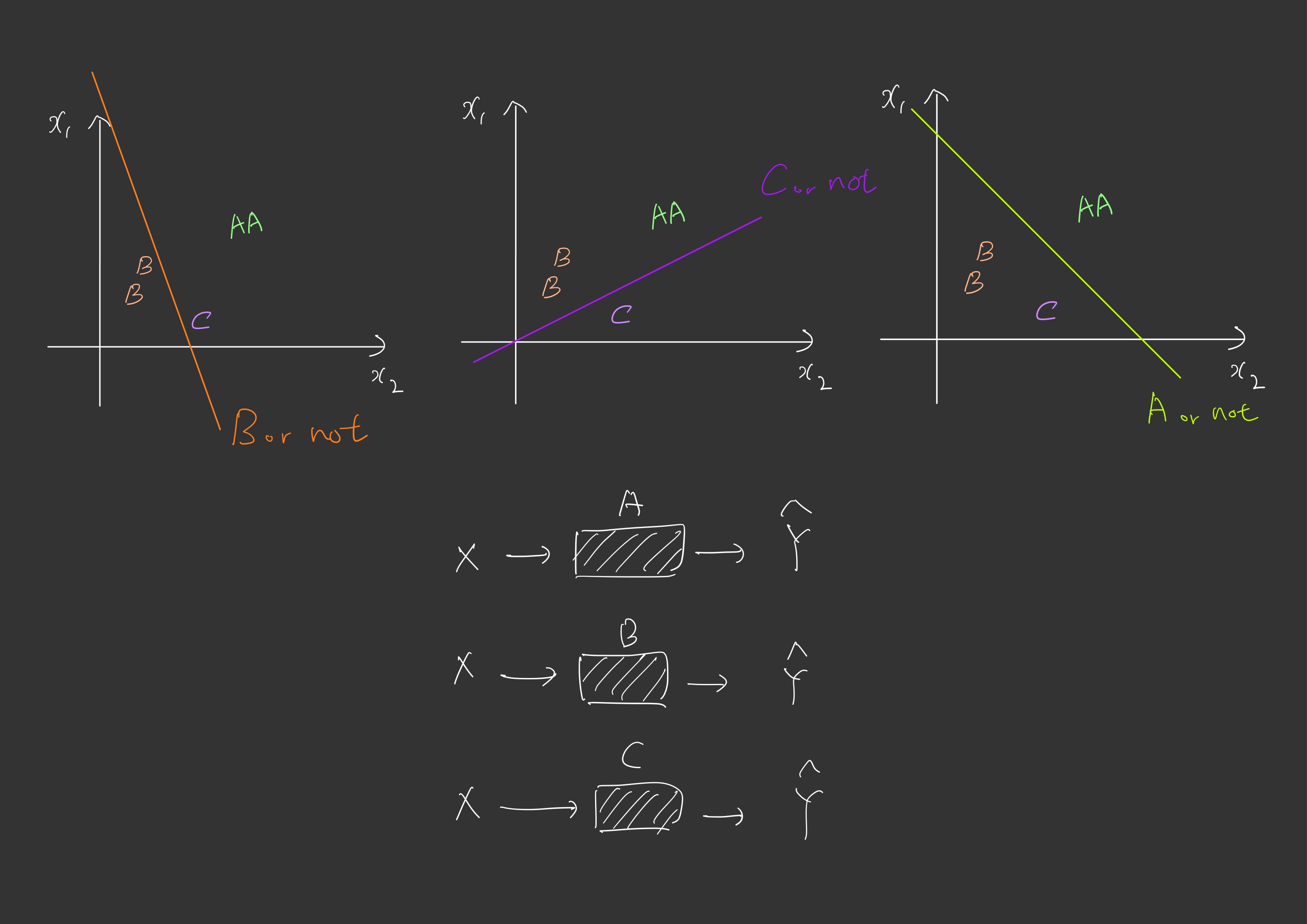
그렇다면 A 분류에 해당하는 선형회귀 하나, B에 하나, C에 하나 이렇게 세가지를 실행해야합니다.

어디서 많이 익숙하지 않으신가요??

바로 다항 선형 회귀내용과 동일합니다. Multivariation Linear Regression 내용이 가물가물 하시면 복습하고 오세요

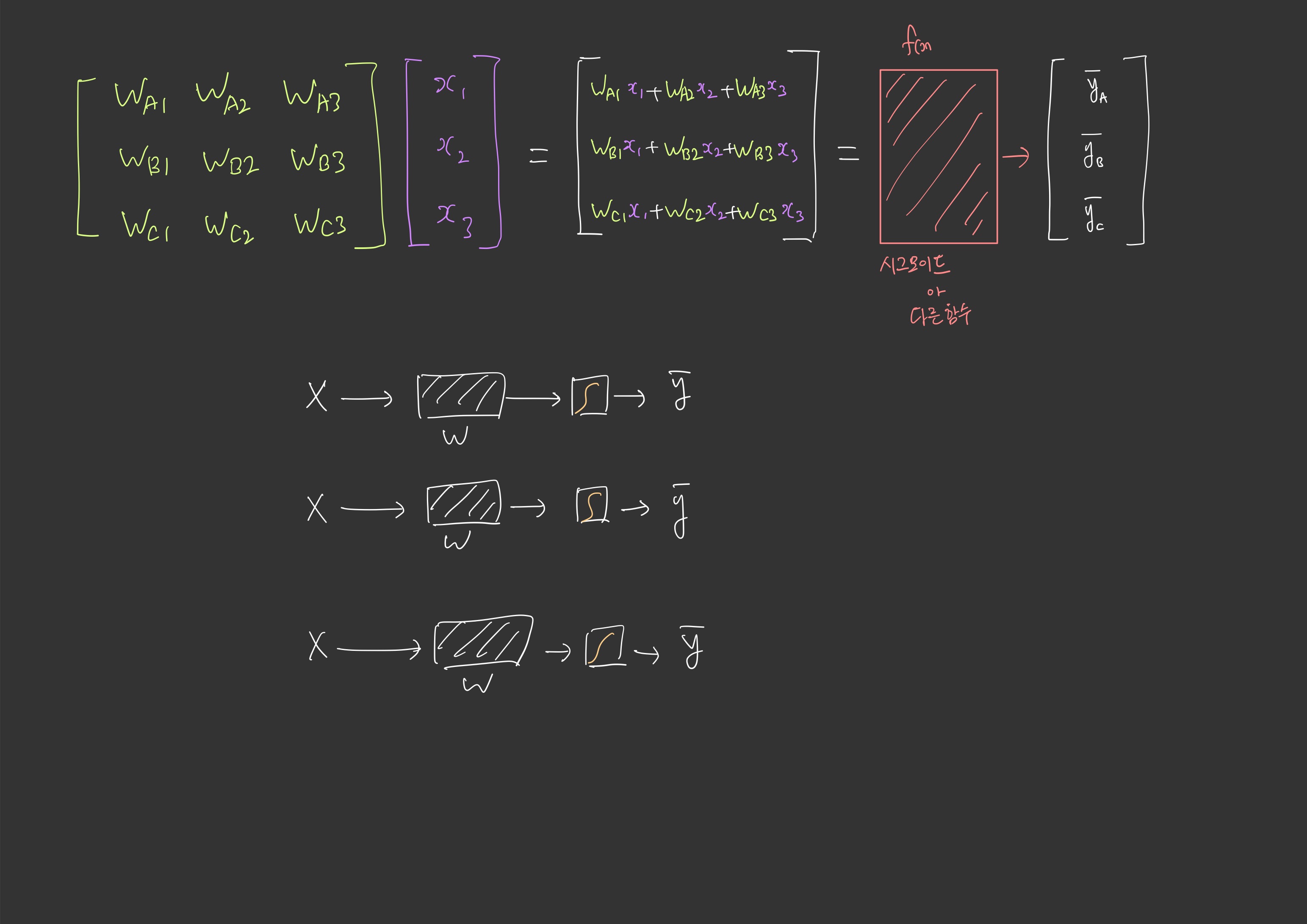
이제 그떄 다항선형회귀와의 차이점이라고 한다면 $\hat{y}$ 출력전에 시그모이드 함수에 대입해준다는 차이점이 있겠습니다.

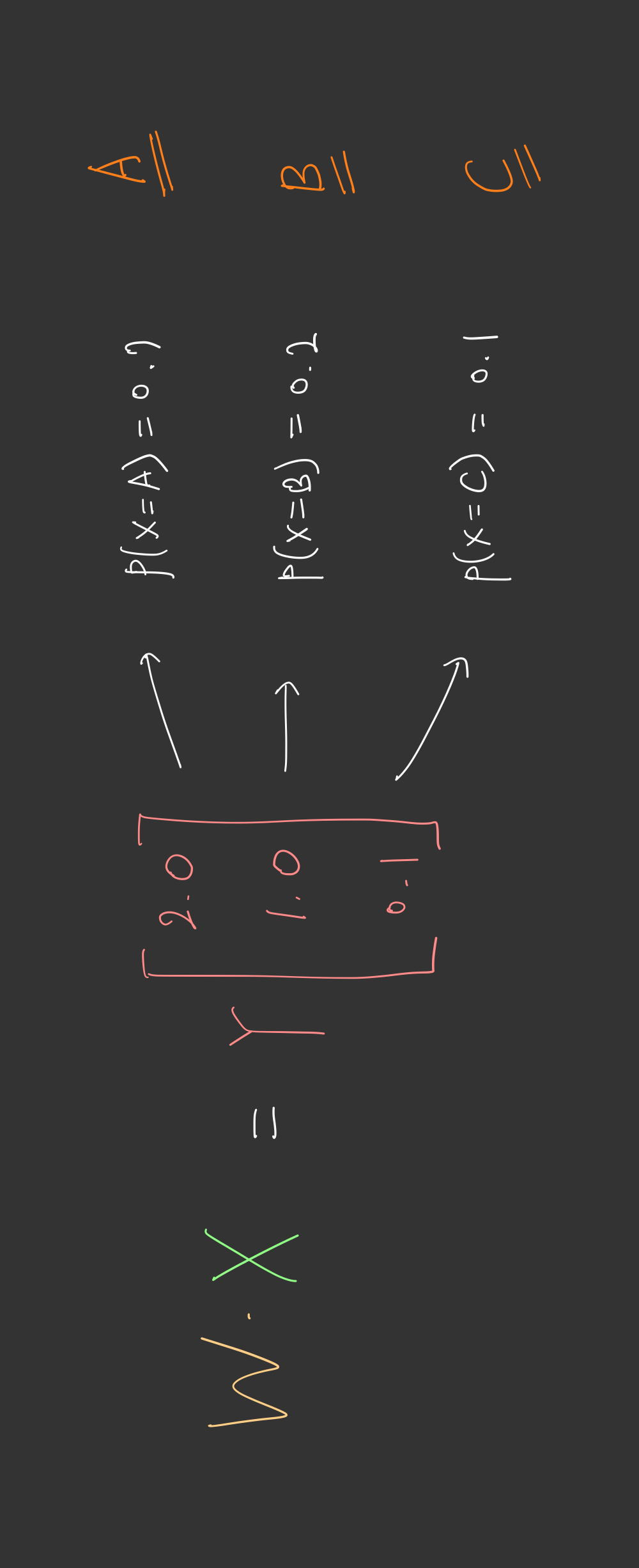
기존 Multivariation Linear Regression 을 통해 나온 결과가 위 그림에서

[2.0, 1.0, 0.1]

입니다. 여기서 우리가 기존에 배웠던 함수인 시그모이드 함수를 사용하게된다면,

[0.8, 0.4, 0.2]

수치는 임의대로 예를들어보았습니다. 이러한 0 부터 1까지의 값이 나오게 될 것입니다. 하지만 우리는 이제 확률적으로 접근을 하고싶기 때문에 아래와 같이 나오게 할 수 있는 방법이 없을까 생각을 하게 됩니다.

A일 확률 = 0.7
B일 확률 = 0.2
C일 확률 = 0.1

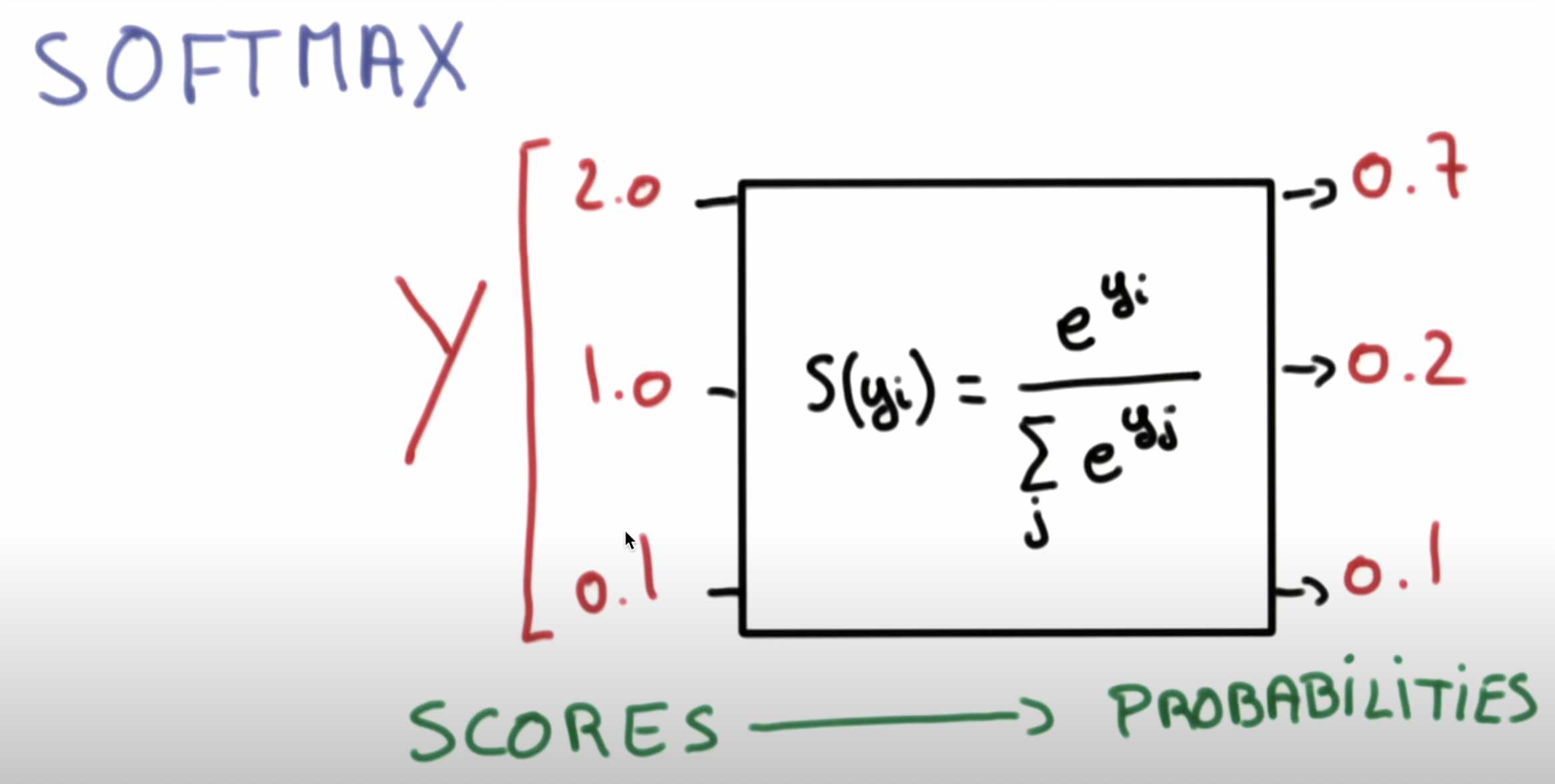
이처럼 만들어주기 위해 필요한 것이 바로 우리가 이제 배워볼 소프트맥스함수인 것입니다!

소프트맥수 함수의 특징답게 각 변수가 0부터1까지의 값을 갖고, 모든 변수의 확률의 합은 1로 일정한 것을 알 수 있습니다. (이산 확률 분포까지 떠올릴 수 있으시면 베스트입니다.)

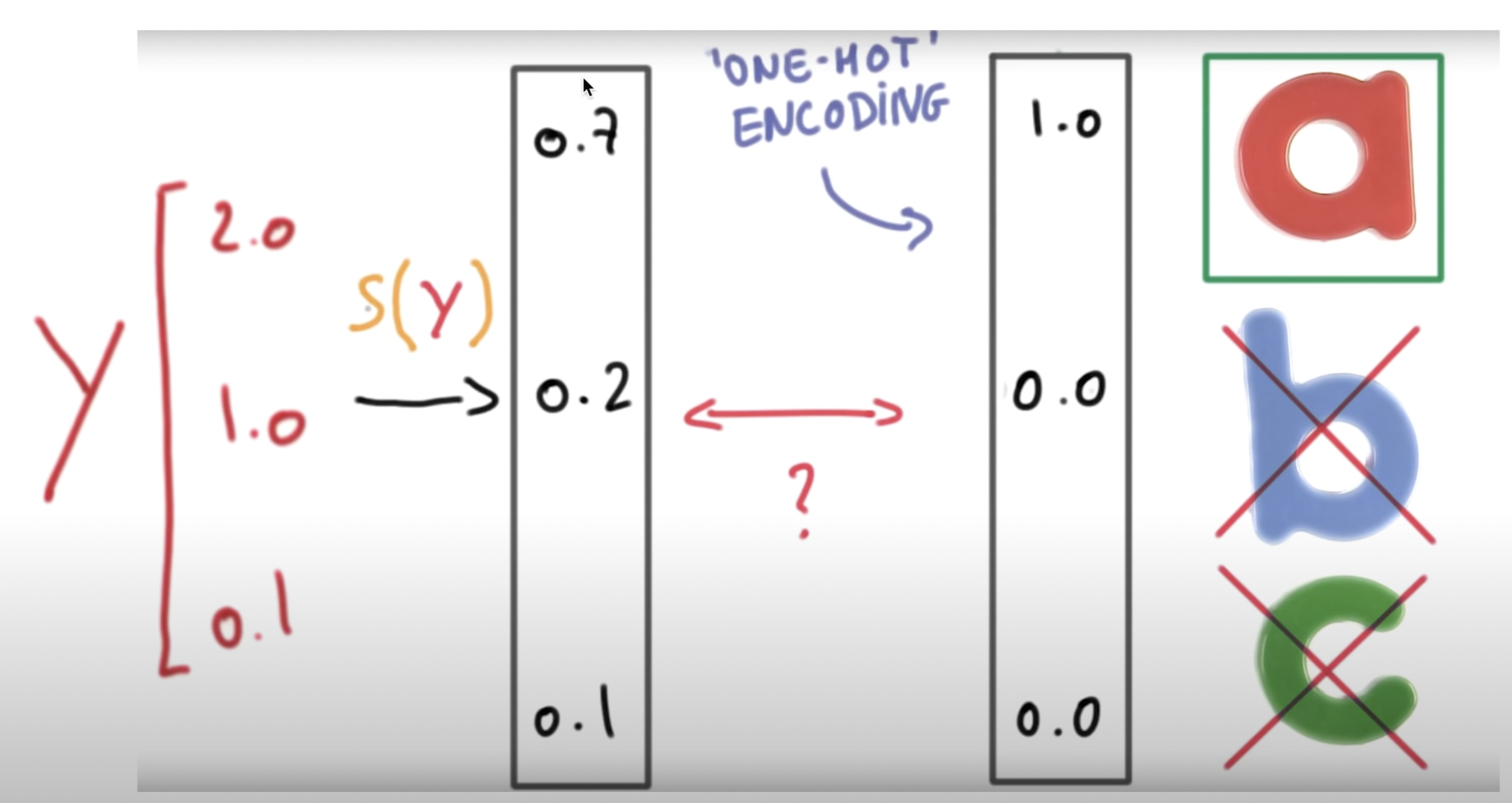
그렇게 출력된 결과를 한번 더 필터를 거칩니다. 원-핫 인코딩으로서 가장 출력값이 높았던 A 등급이다 라는 것을 한눈에 볼 수 있게 됩니다.

Softmax function

소프트맥스 함수는 분류해야하는 정답지(클래스)의 총 개수를 k라고 할 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정합니다.

우선 수식에 대해 설명하고, 그 후에는 그림으로 이해해보겠습니다.

k차원의 벡터에서 i번째 원소를 $z_{j}$, i번째 클래스가 정답일 확률을 $p_{j}$ 로 나타낸다고 하였을 때 소프트맥스 함수는 $p_{j}$ 를 다음과 같이 정의합니다.

\[p_{j}=\frac{e^{z_{j}}}{\sum_{j=1}^{k} e^{z_{j}}}\ \ for\ j=1, 2, ... k\]

만약 변수가 3개인 경우 k=3이므로 3차원 벡터 $z=[z_{1}, z_{2}, z_{3}]$ 의 입력을 받으면 소프트맥스 함수는 아래와 같은 출력을 리턴합니다.

\(softmax(z)=[\frac{e^{z_{1}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{2}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{3}}}{\sum_{j=1}^{3} e^{z_{j}}}] = [p_{1}, p_{2}, p_{3}] = \hat{y} = \text{예측값}\)

Cost function

소프트맥스 회귀에서는 비용 함수로 크로스 엔트로피 함수를 사용합니다. 여기서는 소프트맥스 회귀에서의 크로스 엔트로피 함수뿐만 아니라, 다양한 표기 방법에 대해서 이해해보겠습니다.

Cross-Entropy

아래에서 $y$ 는 실제값을 나타내며 $L_{i}$로도 표현됩니다. $k$ 는 클래스의 개수로 정의합니다.

$y_{j}$ 는 실제값 원-핫 벡터의 $i$ 번째 인덱스를 의미하며, $p_{j}$ 는 샘플 데이터가 $j$ 번째 클래스일 확률을 나타냅니다.

표기에 따라서 $\hat{y}_{j}$ 로 표현하기도 합니다.

\[cost(W) = -\sum_{i=j}^{k}y_{j}\ log(p_{j})\]

이제 이를 n개의 데이터의 대한 평균을 구한다고하면 다음과 같이 표현 할 수 있습니다.

\(cost(W) = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{k}y_{j}^{(i)}\ log(p_{j}^{(i)})\)

Binary Classification(이진분류)의 Cross Entropy

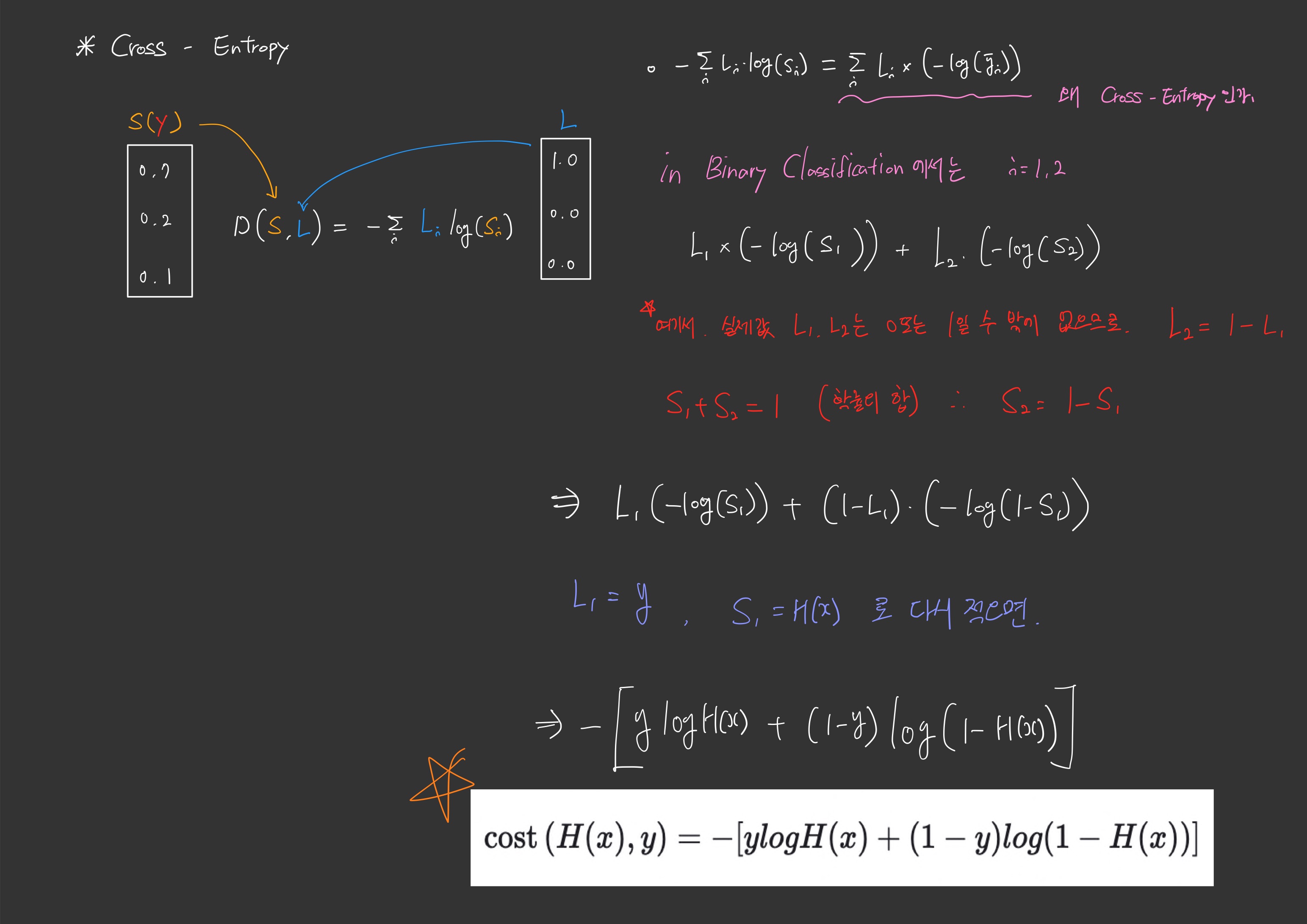
로지스틱회귀에서 배운 손실함수와 소프트맥스분류의 크로스 엔트로피 식은 서로 달라보이지만 사실 같은 식입니다.

단지 이제 우리가 알고 있는 크로스 엔트로피식은 변수가 몇개이든 풀어낼 수 있는 식인 반면, 로지스틱회귀에서의 손실함수는 이진분류의 함수였기 때문에 변수가 2개만 해당되는 식이였던 것입니다.

\[cost(W) = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{k}y_{j}^{(i)}\ log(p_{j}^{(i)}) = -\frac{1}{n} \sum_{i=1}^{n} [y^{(i)}log(p^{(i)}) + (1-y^{(i)})log(1-p^{(i)})]\]

왜 두 식이 같은지는 사진을 참고해주시면 좋겠습니다.

끝!