Lec 07-1: Maximum Liklihood Estimation(MLE)

딥러닝 공부 8일차

Maximum Liklihood Estimation(MLE)

최대 가능도 추정에 대해서 알아보겠습니다.

다음 그림과 같이 압정을 떨어뜨렸을 때, 똑바로 서거나 비스듬히 눕거나 두가지 종류만 있다고 가정해보겠습니다! (실제로는 바닥에 박히는 등 다른 경우의 수고 있겠지만요)

사진에서 처음보는 용어가 등장합니다. 베르누이? 유체역학에서 배웠던 그 베르누이인가… 네 개소리구요

베르누이 시행이란?

결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행(Bernoulli trial)이라고 한다.

예를 들어 동전을 한 번 던져 앞면(H:Head)이 나오거나 뒷면(T:Tail)이 나오게 하는 것도 베르누이 시행이다.

그래서 위에서 압정이 떨어지는 경우의수를 두가지로만 제한한 이유입니다.

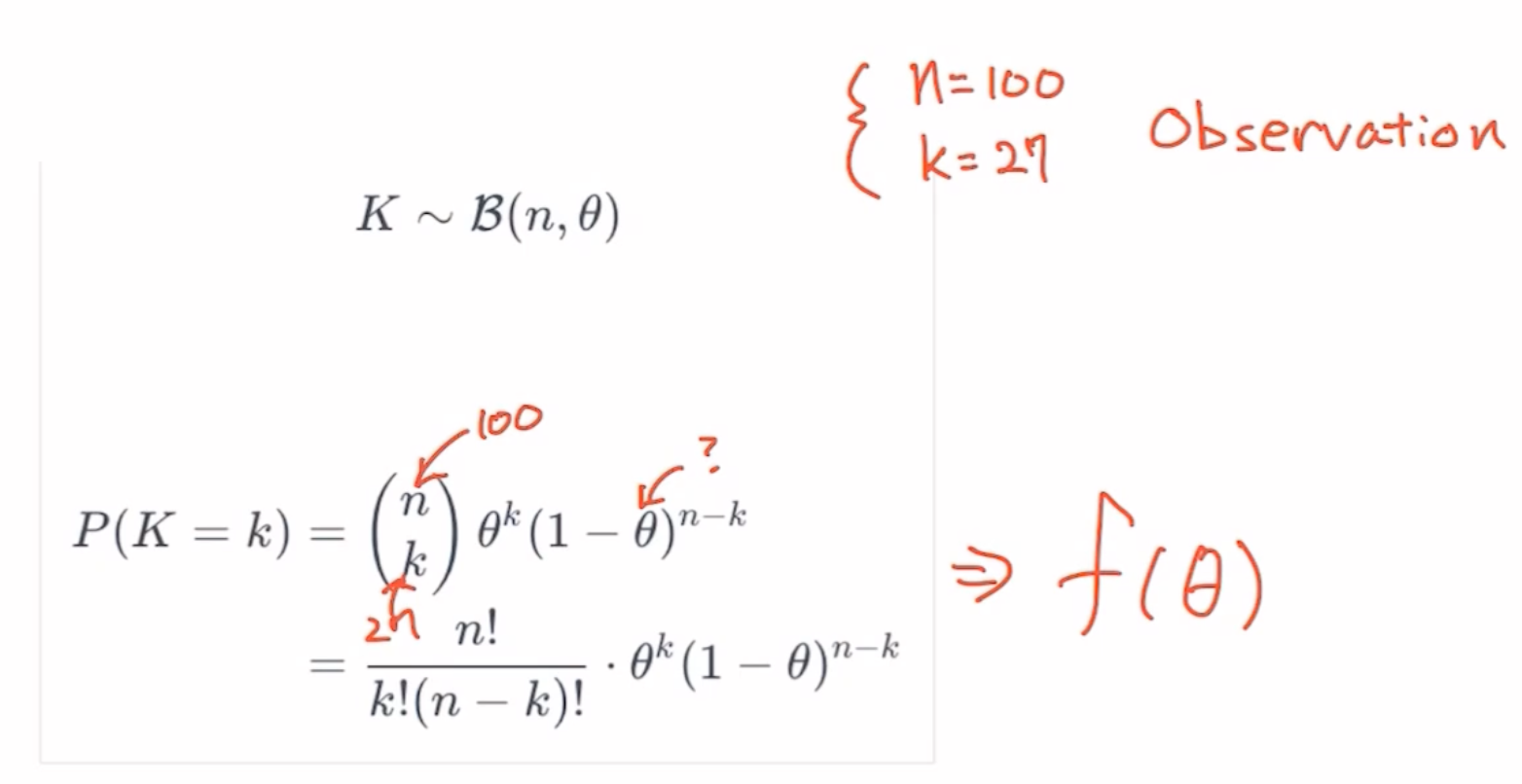
두가지 경우의수만 있는 이산확률분포에서의 확률을 구하는 식입니다.

조합(Combination)을 떠올리실 수 있으면 베스트입니다. n번의 시행중 원하는 사건이 k번 일어날 확률입니다.

그림에서의 $\theta$가 원하는 사건이 일어날 확률이고, 베르누이 시행이기 때문에 나머지 사건의 확률은 $(1-\theta)$ 이 되겠습니다.

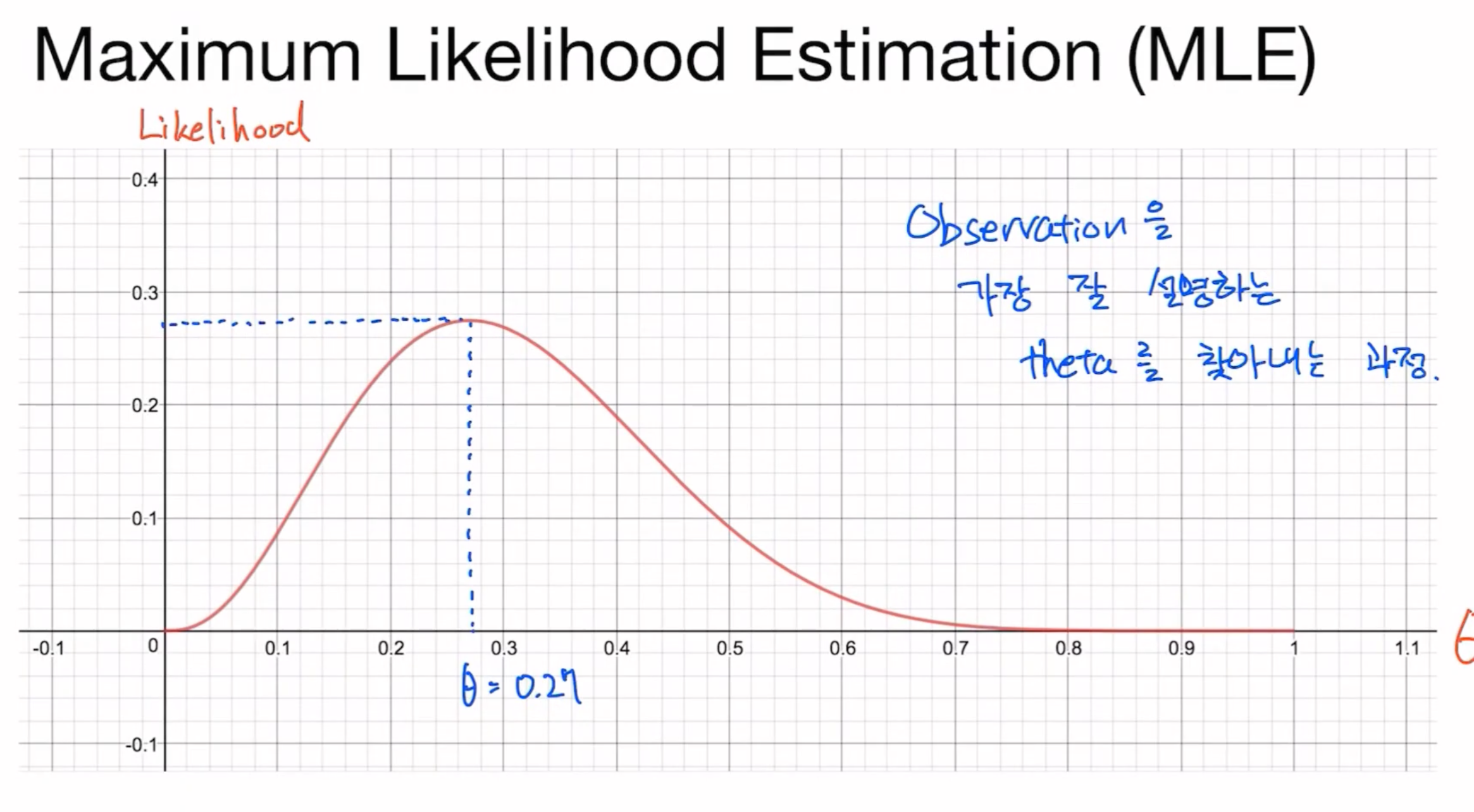
그렇다면 그 확률이 최대가 되는 지점을 찾는 것이 우리의 목표인데 그 최대인 지점은 어떻게 찾을 수 있을까요?

Gradient Ascent

우리가 그동안 손실함수에서 최소가되는 cost 값을 찾기 위해 Gradient Descent 방식으로 최저점을 찾았다면 이번에는 가능도함수의 최대지점을 찾기 위해 반대의 방식인 Gradient Ascent 방식을 사용합니다.

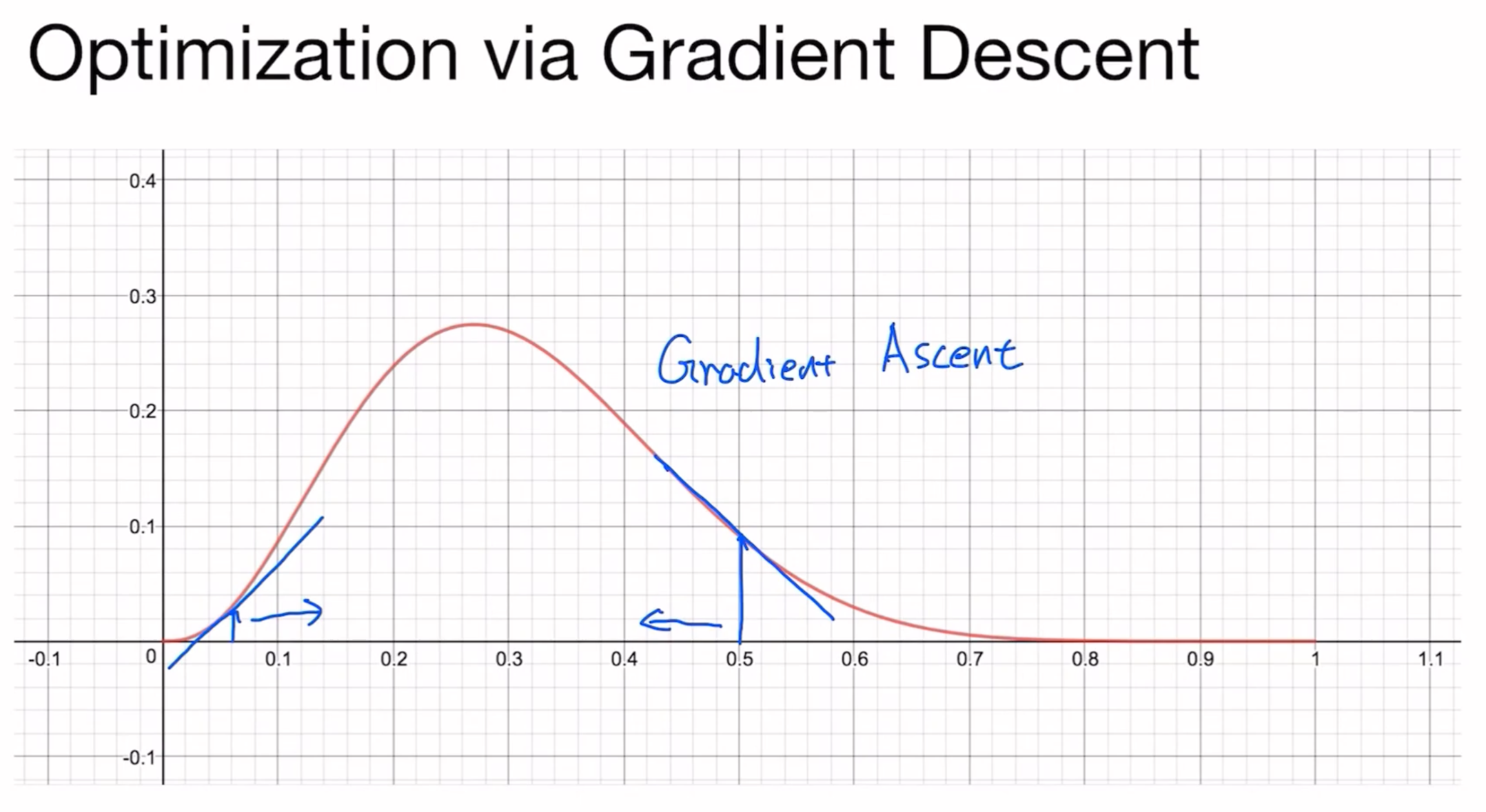
작동원리 👈 Gradient Descent 방식의 상세한 설명이 나와있습니다. 보고 오시면 좋을 것 같습니다 😽

이제 우리는 손실함수를 최소화 시키거나, 관측한 함수의 최대 가능도가 어디인지 찾을 수 있게 되었습니다.

이렇게 데이터를 최소 손실, 최대 가능도로 학습시키다보면 Overfitting 을 피해갈 수가 없게 됩니다.

이 overfitting(과적합)에 대해서 다음 글에서 다뤄보도록 하겠습니다.

끝!