Lec 08-1: Perceptron

딥러닝 공부 11일차

Perceptron(퍼셉트론)

본격적으로 퍼셉트론에 대해서 공부하기 전에, 인공 신경망에 대해서 조금 알아보겠습니다.

신경세포 중 뉴런에서 일어나는 일을 살펴보겠습니다. 뉴런은 신호를 전달 받아서 전달해주는 역할을 합니다.

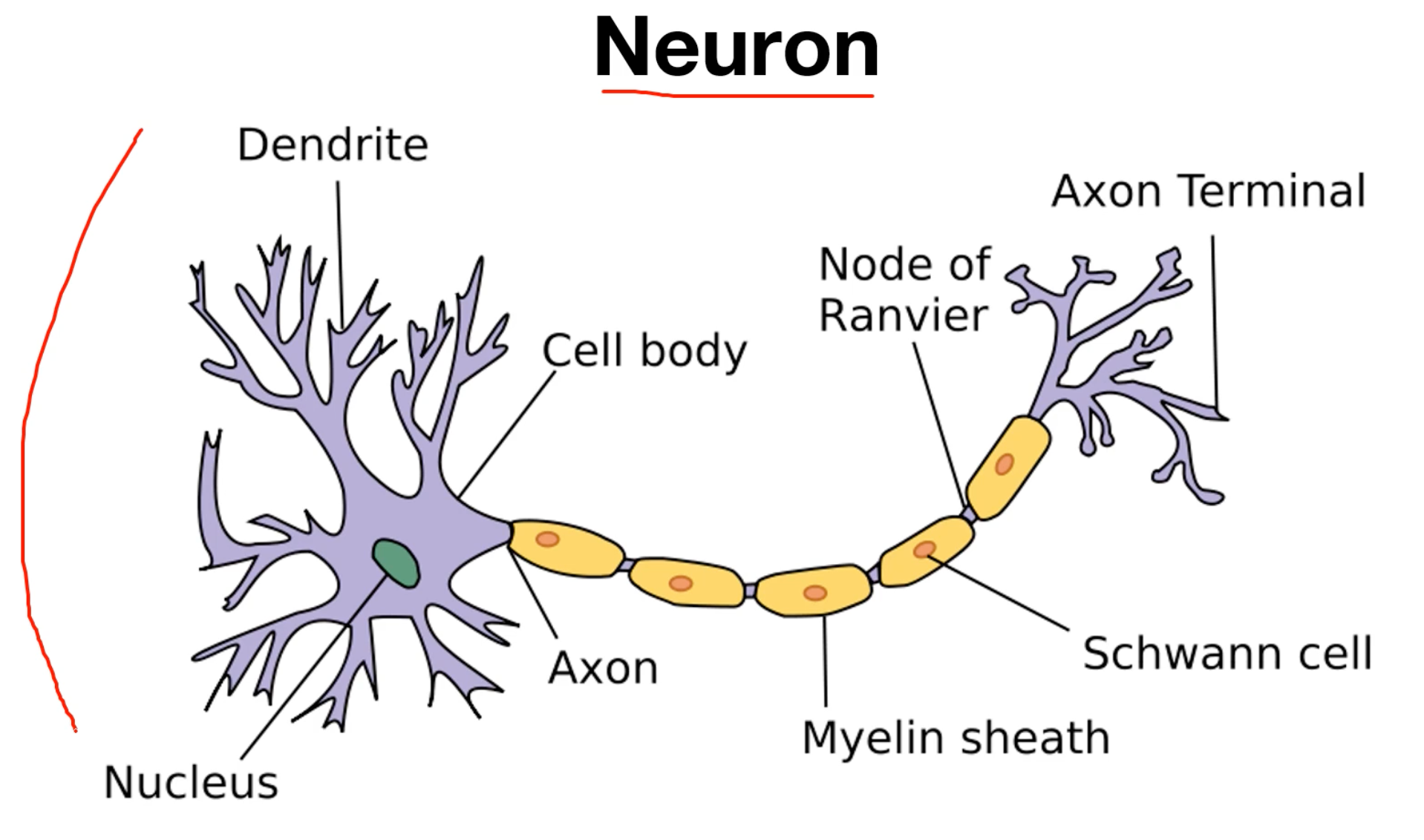
사진상의 왼쪽부분이 신호를 전달 받는 부분이고 오른쪽 부분이 신호를 전달 해주는 부분입니다.

뉴런은 어떠한 임계치 이하의 값은 전달하지 않고, 임계치 이상의 신호만 전달하는 특징이 있습니다.

이 특징이 이제 배울 퍼셉트론의 주요한 성질로 사용될 것입니다. 기억해주세요~

결론적으로 퍼셉트론은 다수 입력으로 하나의 결과를 내보내는 알고리즘입니다.

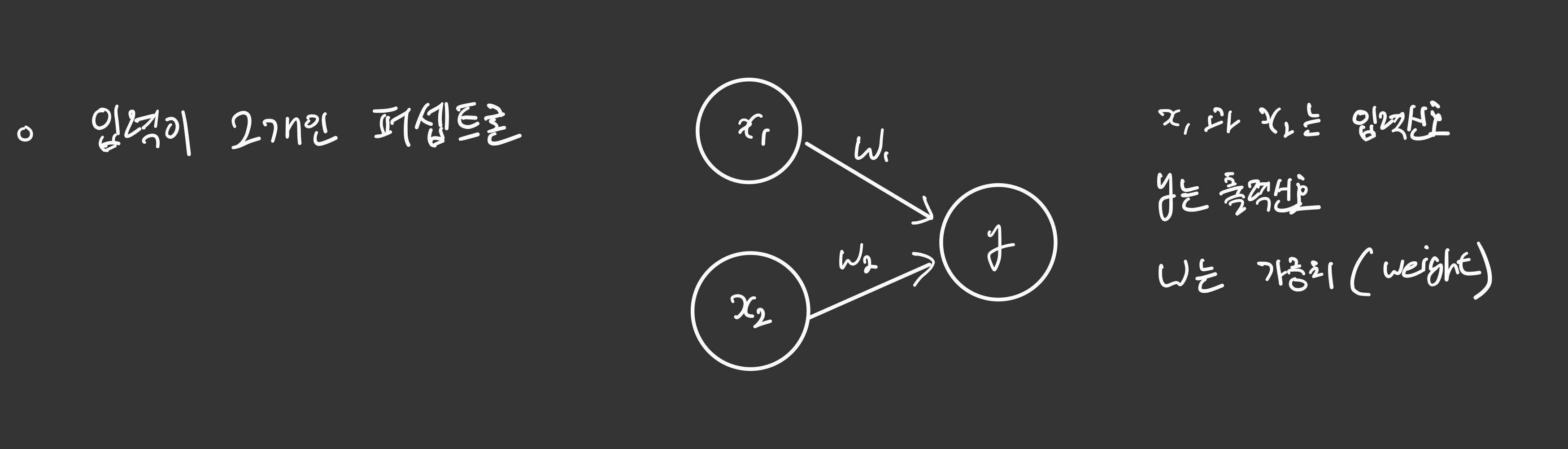
가볍게 입력이 두개인 퍼셉트론입니다.

보통 x를 입력값, y를 출력값이라고 합니다. 그래서 $y=W_{1}x_{1}+W_{2}x_{2}$ 정도로 표현할 수 있겠습니다. (참고로 이 퍼셉트론은 편향이 없는 퍼셉트론인 것입니다.)

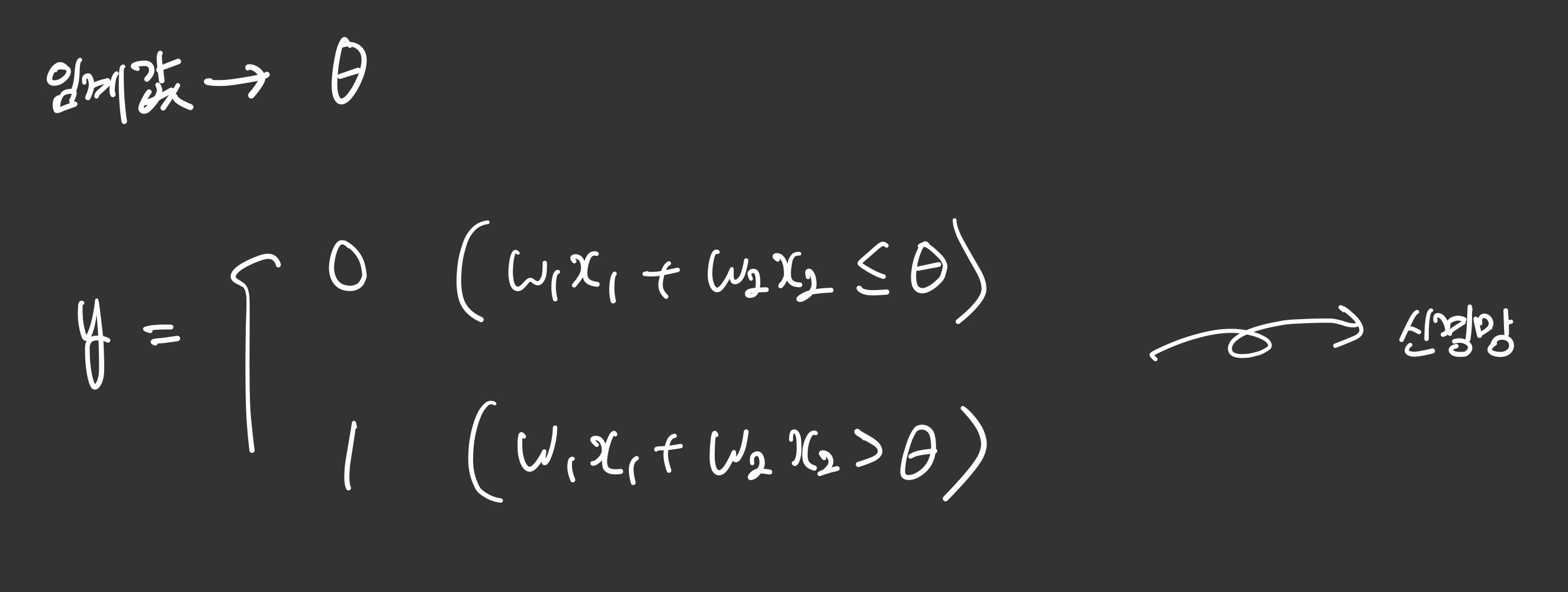
그래서 아까 뉴런의 특징으로 중요하다고 했던 부분이 있었죠? 일정한 임계값 이상일 때 신호를 출력한다고 했던 특징이 여기있습니다.

$\theta$를 임계값이라고 할 때, $W_{1}x_{1}+W_{2}x_{2}\gt\theta$ 일 때, 출력값 1이 나오게 됩니다.

정리하면

\[if \sum_i^{n} W_{i}x_{i}\ ≥ \theta → y=1\] \[if \sum_i^{n} W_{i}x_{i}\ < \theta → y=0\]

이제 여기서 나온 임계값 $\theta$가 사실 좌변으로 넘기면 편향 $b$(bias) 역할을 하게 되는 것입니다.

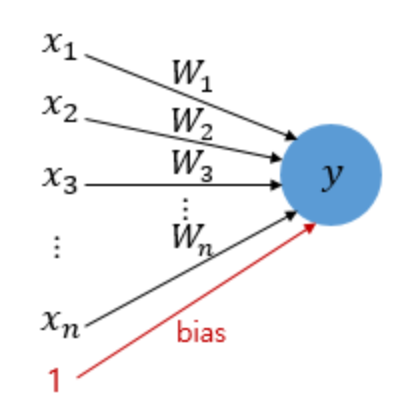
그래서 편향값은 입력값을 1로 표현합니다.

\[if \sum_i^{n} W_{i}x_{i} + b ≥ 0 → y=1\] \[if \sum_i^{n} W_{i}x_{i} + b < 0 → y=0\]

이렇게 뉴런에서 출력값을 변경시키는 함수를 활성화 함수(Activation Function)이라고 합니다.

논리회로

And 게이트

그간 프로그래밍언어에서 접해봤을 법한 내용입니다. And 게이트는 아래 그림처럼 모두 1일 경우 1을 출력하는 논리회로입니다.

and 게이트가 활성화되는 경우의 예시입니다.

\((W_{1},W_{2},\theta) = (0.5, 0.5, 0.8)\) 위 예시의 경우 직접 계산해보면 1이 출력 된다는 것을 생각해보실 수 있습니다.

\[0.5*1+0.5*1\gt0.8\]

코드로 구현해보면 다음과 같습니다.

def AND_gate(x1, x2):
    w1=0.5
    w2=0.5
    b=-0.7
    result = x1*w1 + x2*w2 + b
    if result <= 0:
        return 0
    else:
        return 1

AND_gate(0, 0), AND_gate(0, 1), AND_gate(1, 0), AND_gate(1, 1)

(0, 0, 0, 1)

Or 게이트

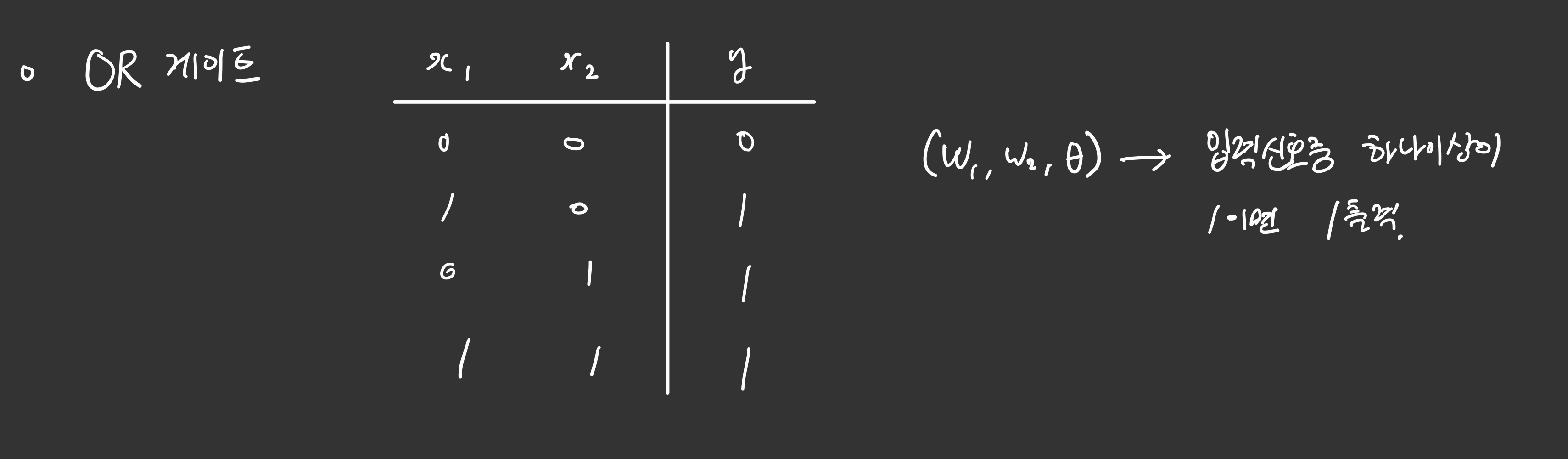
1이 섞이기만하면 1을 출력하는 논리회로입니다.

코드로 구현해보면 다음과 같습니다.

def OR_gate(x1, x2):
    w1=0.6
    w2=0.6
    b=-0.5
    result = x1*w1 + x2*w2 + b
    if result <= 0:
        return 0
    else:
        return 1

OR_gate(0, 0), OR_gate(0, 1), OR_gate(1, 0), OR_gate(1, 1)

(0, 1, 1, 1)

NAND 게이트

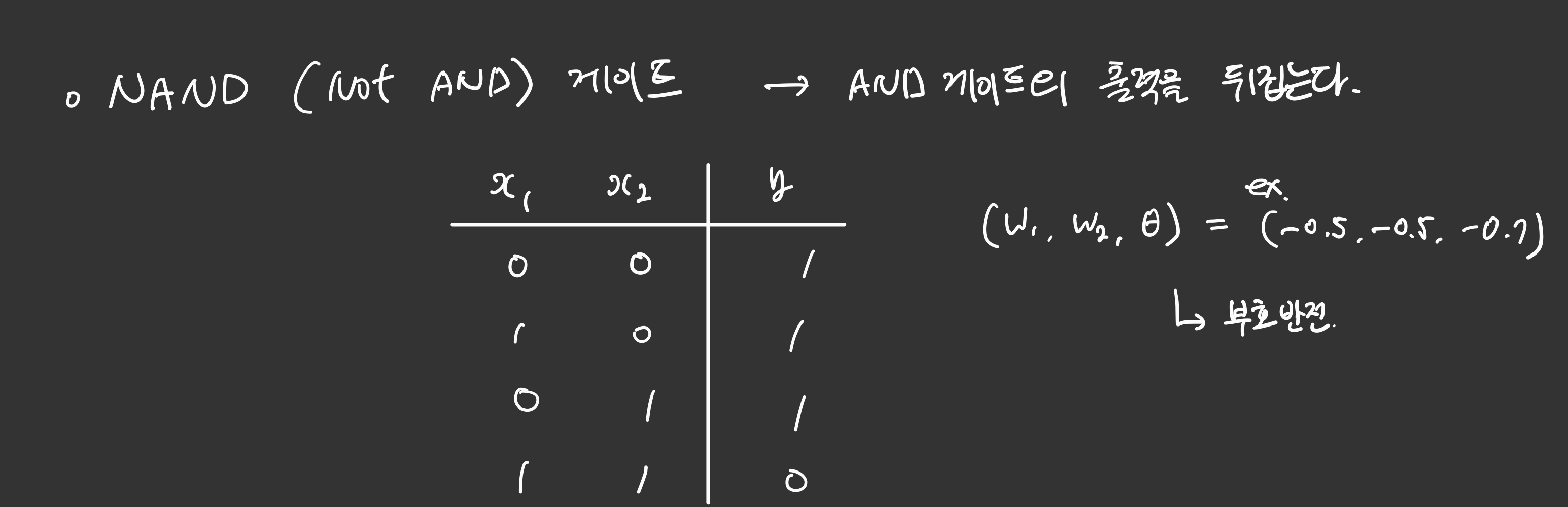
NAND 게이트는 AND 게이트의 출력을 뒤집어주면 됩니다.

코드로 구현해보면 다음과 같습니다.

def NAND_gate(x1, x2):
    w1=-0.5
    w2=-0.5
    b=0.7
    result = x1*w1 + x2*w2 + b
    if result <= 0:
        return 0
    else:
        return 1

NAND_gate(0, 0), NAND_gate(0, 1), NAND_gate(1, 0), NAND_gate(1, 1)

(1, 1, 1, 0)

XOR 게이트

베타적 논리합이라고도 하는 XOR 게이트입니다. XOR 게이트는 이전까지 배운 퍼셉트론으로는 구현할 수가 없습니다.

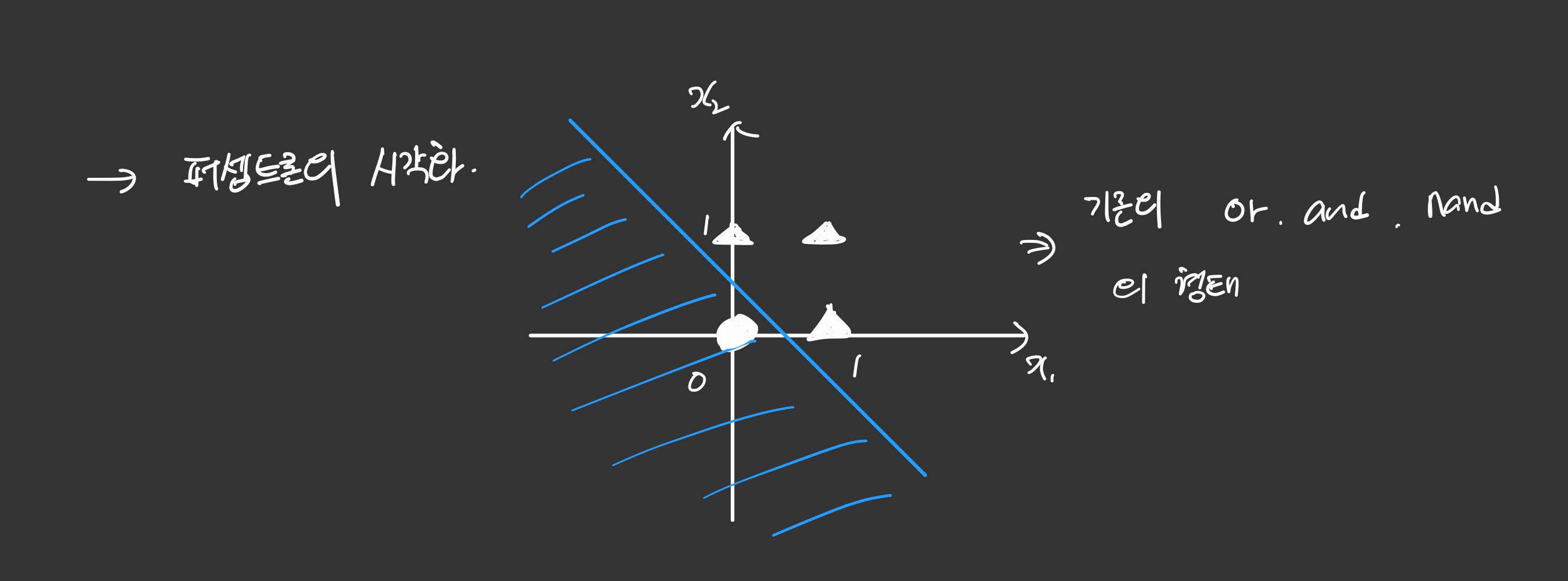
퍼셉트론들을 시각화해서 왜 안되는지 확인해볼까요?

퍼셉트론의 시각화 및 다층퍼셉트론의 필요성

기존의 or, and, nand 의 형태는 단층 퍼셉트론, 즉 직선의 형태로 구현이 가능했습니다.

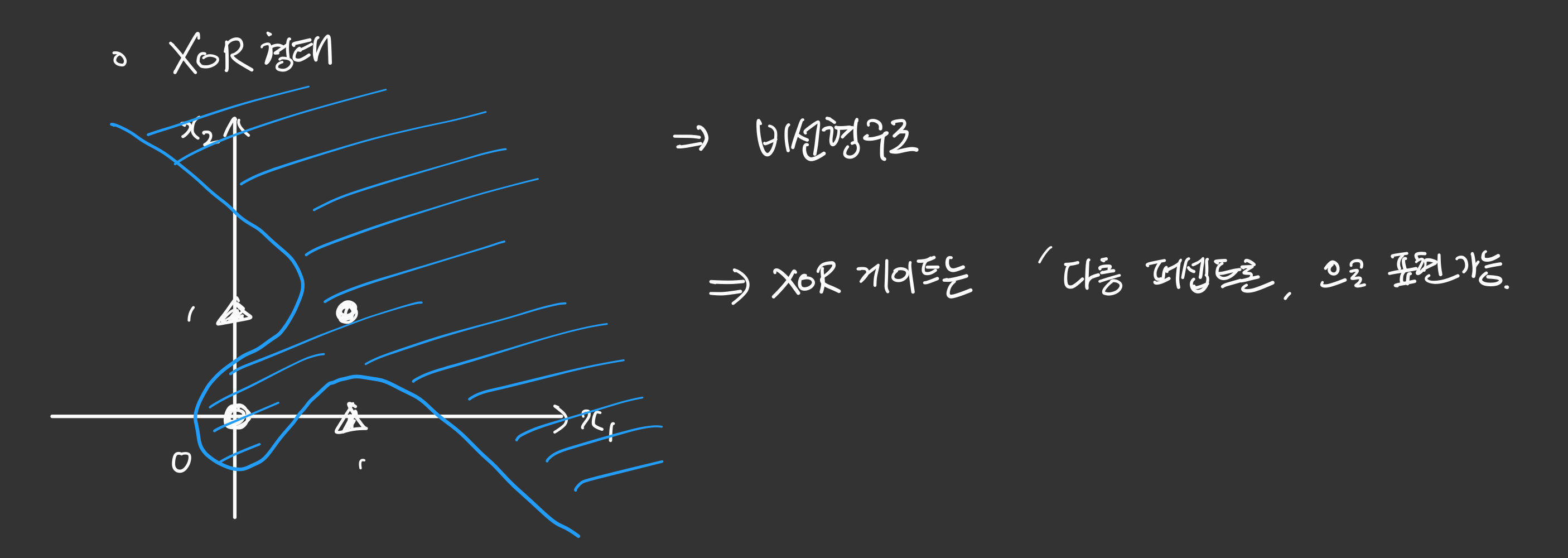
XOR 형태는 그림처럼 직선으로 표현할 수가 없습니다. 그래서 비선형구조가 필요하고 그러한 비선형구조는 ‘다층 퍼셉트론’ 으로 표현이 가능합니다.

다층 퍼셉트론의 예시로 XoR 게이트는 아래 그림과 같이 표현이 가능합니다.

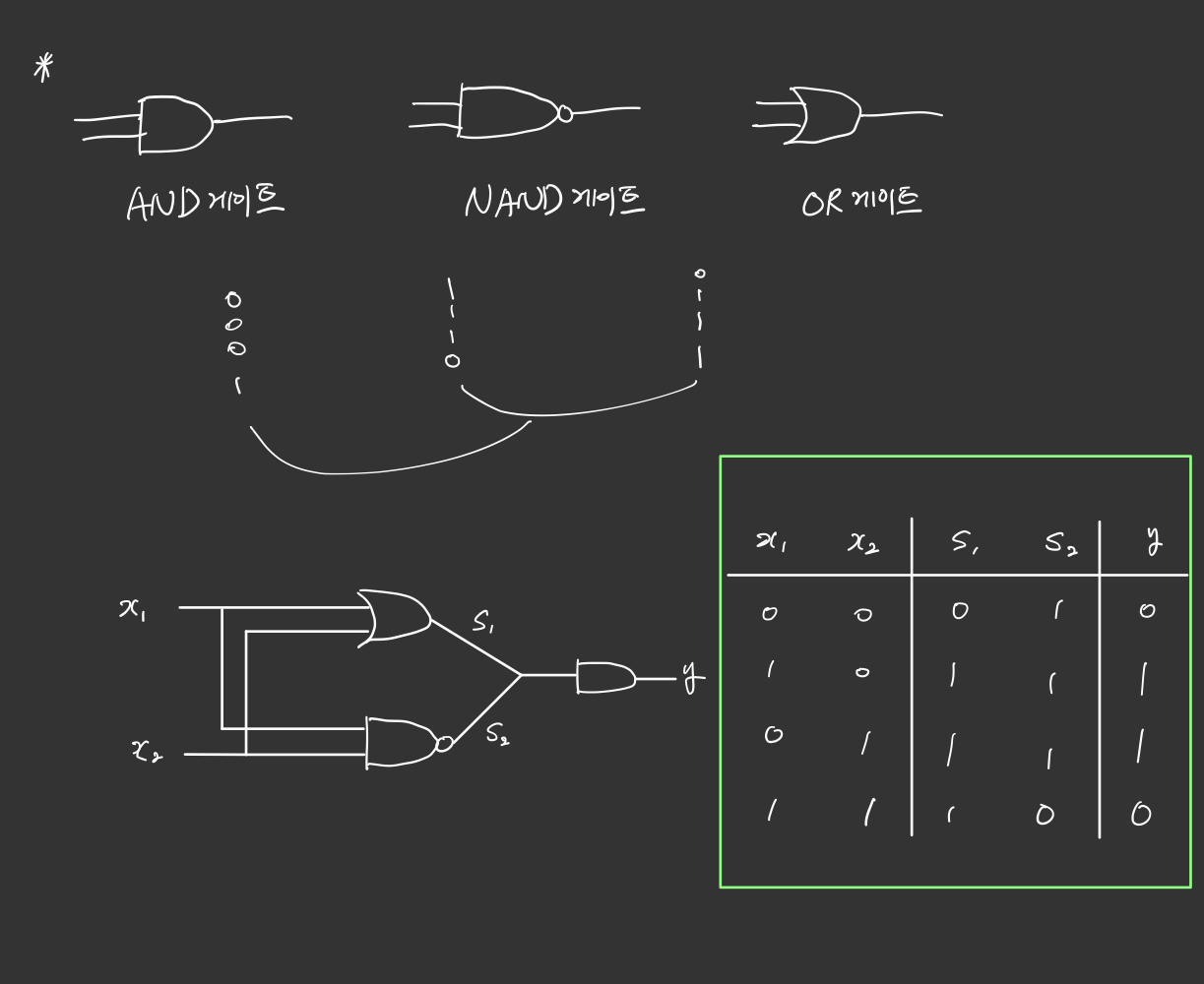
MultiLayer Perceptron, MLP(다층 퍼셉트론)

XOR 게이트는 기존의 AND, NAND, OR 게이트를 조합하면 만들 수 있습니다. 퍼셉트론 관점에서 말하면, 층을 더 쌓으면 만들 수 있습니다.

다층 퍼셉트론과 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가하였다는 점입니다.

이렇게 입력층과 출력층 사이에 존재하는 층을 은닉층(hidden layer)이라고 합니다. 즉, 다층 퍼셉트론은 중간에 은닉층이 존재한다는 점이 단층 퍼셉트론과 다릅니다.

다층 퍼셉트론은 줄여서 MLP라고도 부릅니다.

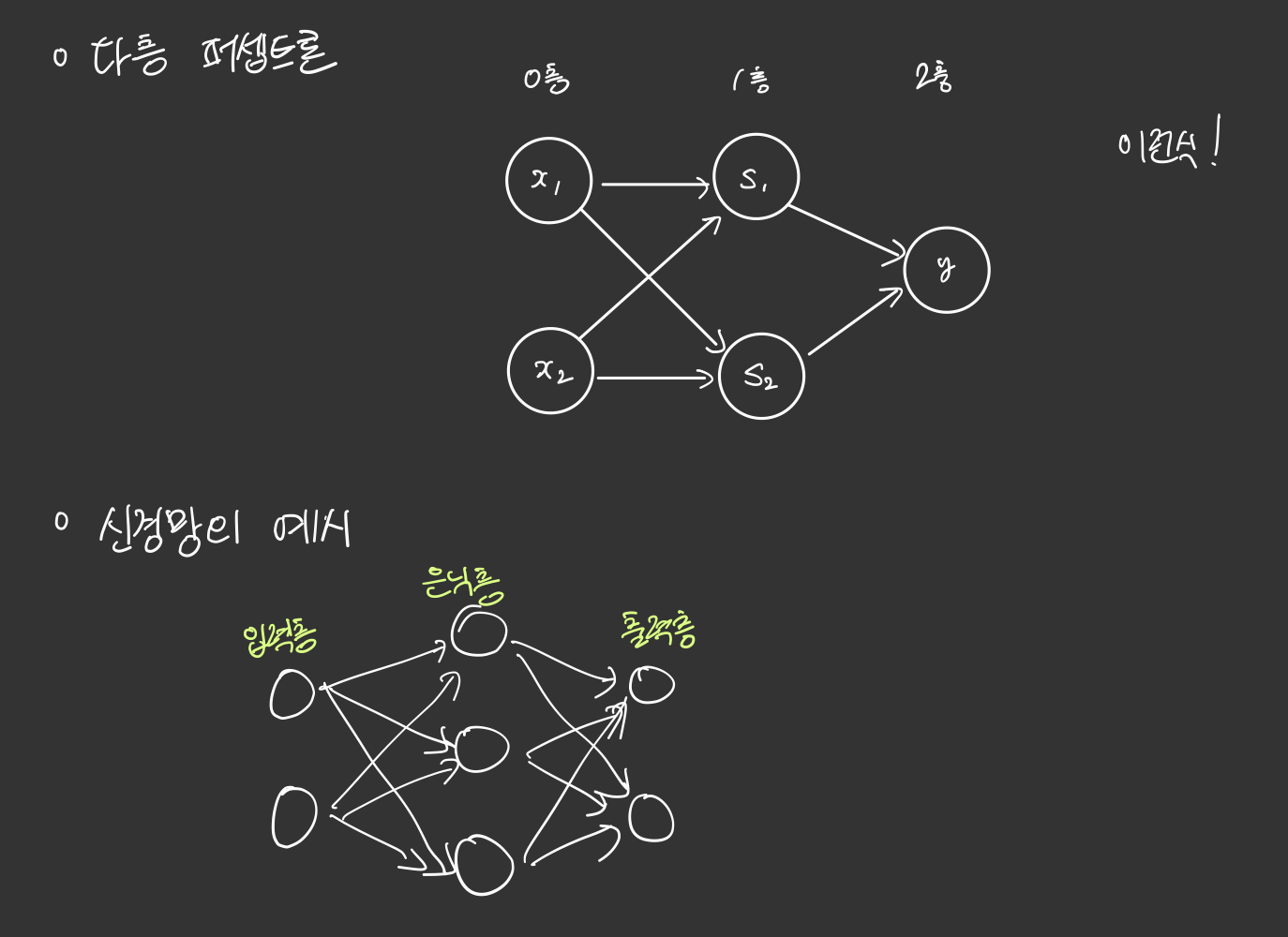
은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN) 이라고 합니다.

지금까지는 OR, AND, XOR 게이트 등. 퍼셉트론이 가야할 정답을 참고로 퍼셉트론이 정답을 출력할 때까지 가중치를 바꿔보면서 맞는 가중치를 찾았습니다.

즉, 가중치를 수동으로 찾았습니다.

하지만 이제는 기계가 가중치를 스스로 찾아내도록 자동화시켜야하는데, 이것이 머신 러닝에서 말하는 학습(training) 단계에 해당됩니다.

앞서 선형 회귀와 로지스틱 회귀에서 보았듯이 손실 함수(Loss function) 와 옵티마이저(Optimizer) 를 사용합니다.

그리고 만약 학습을 시키는 인공 신경망이 심층 신경망일 경우에는 이를 심층 신경망을 학습시킨다고 하여, 딥 러닝(Deep Learning) 이라고 합니다.

다음 글에서 다중 퍼셉트론에 대해서 더 자세히 알아보겠습니다.

끝!

참고문헌, [밑바닥부터 시작하는 딥러닝]