Lec 08-2: MultiLayer Perceptron(MLP) & Backpropagation

딥러닝 공부 12일차

BackPropagation(역전파)

인공 신경망을 열심히 만들고 돌렸는데, 예측값과 실제값이 다를 경우에 우리는 입력값을 다시 조정하여서 적절한 W 와 b 값을 다시 찾아야합니다.

하지만 이런 과정은 결코 쉽지않았고 과거의 DNN의 큰 문제로 남겨져 있었습니다.

하지만 현재, 이러한 문제는 BackPropagation, 역전파라는 방법으로 해결할 수 있습니다.

인공 신경망의 이해(Neural Network Overview)

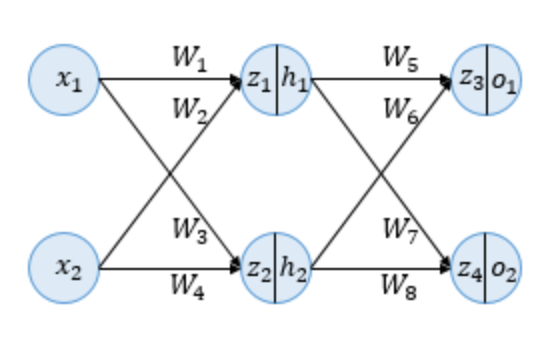
예제를 위해 사용될 인공신경망입니다. 입력층이 2개, 은닉층이 2개, 출력층이 2개입니다.

z는 이전층의 모든 입력이 각각의 가중치와 곱해진 값들의 합을 의미합니다. 이 값은 아직 활성화함수를 거치기 전 상태입니다.

이제 h값을 통해 활성화함수를 거치게 됩니다. 우리는 활성화함수로 시그모이드함수를 사용할 것 입니다.

o 값은 출력값을 의미합니다.

순전파(Forward Propagation)

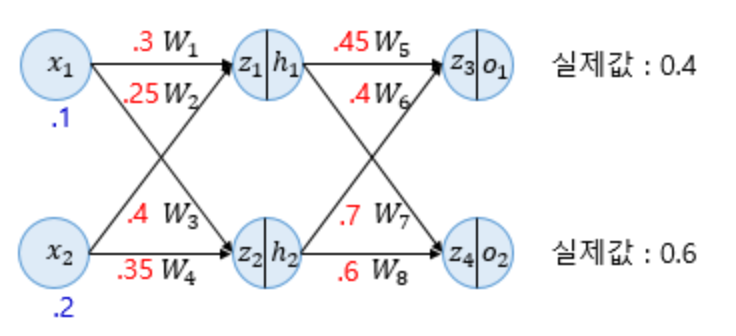
주어진 값이 위 그림과 같을 때, 순전파를 진행해보겠습니다. 소수점 앞의 0은 생략된 사진입니다.

$z_{1}$ 과 $z_{2}$ 는 입력층의 입력값들을 받습니다.

\[z_{1}=W_{1}x_{1} + W_{2}x_{2}=0.3 \text{×} 0.1 + 0.25 \text{×} 0.2= 0.08\] \[z_{2}=W_{3}x_{1} + W_{4}x_{2}=0.4 \text{×} 0.1 + 0.35 \text{×} 0.2= 0.11\]

이제 각각의 $z_{1}$ 과 $z_{2}$ 는 은닉층의 활성화함수를 거치게 됩니다.

\[h_{1}=sigmoid(z_{1}) = 0.51998934\] \[h_{2}=sigmoid(z_{2}) = 0.52747230\]

이제 $h_{1}$ 과 $h_{2}$ 는 이제 출력층의 뉴런으로 향하게 되는데, 다시 각각의 가중치와 곱해져서 전달이 되게 됩니다.

\[z_{3}=W_{5}h_{1}+W_{6}h_{2} = 0.45 \text{×} h_{1} + 0.4 \text{×} h_{2} = 0.44498412\] \[z_{4}=W_{7}h_{1}+W_{8}h_{2} = 0.7 \text{×} h_{1} + 0.6 \text{×} h_{2} = 0.68047592\]

$z_{3}$ 와 $z_{4}$ 는 출력층 뉴런에서 시그모이드 함수를 지나게되고, 이 값들은 최종적으로 계산된 출력값입니다. 즉, 예측값입니다.

\[o_{1}=sigmoid(z_{3})=0.60944600\] \[o_{2}=sigmoid(z_{4})=0.66384491\]

이제 필요한 것은, 예측갑과 실제값의 오차를 계산하기 위한 오차함수, 즉 손실함수를 선택하는 것입니다.

여기서는 MSE 방식을 사용하도록 하겠습니다. 예측값을 output, 실제값을 target이라고 표현하겠습니다.

\[E_{o1}=\frac{1}{2}(target_{o1}-output_{o1})^{2}=0.02193381\] \[E_{o2}=\frac{1}{2}(target_{o2}-output_{o2})^{2}=0.00203809\] \[E_{total}=E_{o1}+E_{o2}=0.02397190\]

오차의 총합은 위의 마지막식과 같습니다.

역전파 1단계(BackPropagation Step1)

순전파가 입력층에서 출력층으로 향한다면 역전파는 반대로 출력층에서 입력층 방향으로 계산해가면서 가중치를 업데이트 해갑니다.

다층 퍼셉트론에서 은닉층이 많을수록 역전파의 단계수가 많아집니다. 은닉층이 너무 많을 경우는 역전파 방법이 별로 효과가 없습니다.

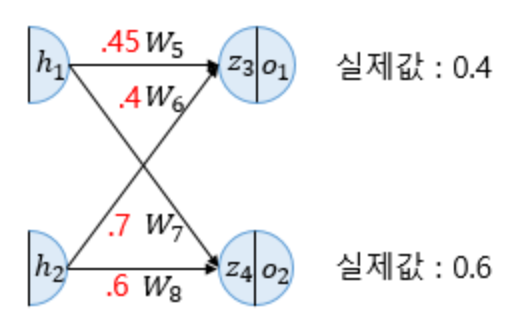
역전파 1단계에서 업데이트 해야 할 가중치는 $W_{5}, W_{6}, W_{7}, W_{8}$ 총 4개 입니다.

모든 역전파의 원리는 동일합니다.

$W_{5}$ 에 대해서 먼저 업데이트를 진행해보겠습니다. $W_{5}$ 를 업데이트 하기 위해서 $\frac{∂E_{total}}{∂W_{5}}$ 를 계산해야 합니다.

$\frac{∂E_{total}}{∂W_{5}}$ 를 계산하기 위해서는 Chain Rule(합성합수미분)을 이용하여 계산할 수 있습니다.

\[\frac{∂E_{total}}{∂W_{5}} = \frac{∂E_{total}}{∂o_{1}} \text{×} \frac{∂o_{1}}{∂z_{3}} \text{×} \frac{∂z_{3}}{∂W_{5}}\]

위 식에서 각각의 항을 하나씩 계산해봅시다. 오차의 총합은 다음과 같았었습니다.

\[E_{total}=\frac{1}{2}(target_{o1}-output_{o1})^{2} + \frac{1}{2}(target_{o2}-output_{o2})^{2}\]

이제 첫번째 항을 계산해보면 $E_{total}$ 에 대한 $W_{5}$ 방향으로의 편미분이므로

\[\frac{∂E_{total}}{∂o_{1}}=2 \text{×} \frac{1}{2}(target_{o1}-output_{o1})^{2-1} \text{×} (-1) = -(0.4-0.60944600) = 0.20944600\]

과 같습니다.

시그모이드함수의 미분

두번째 항을 계산하기 앞서 시그모이드 함수를 미분해보겠습니다.

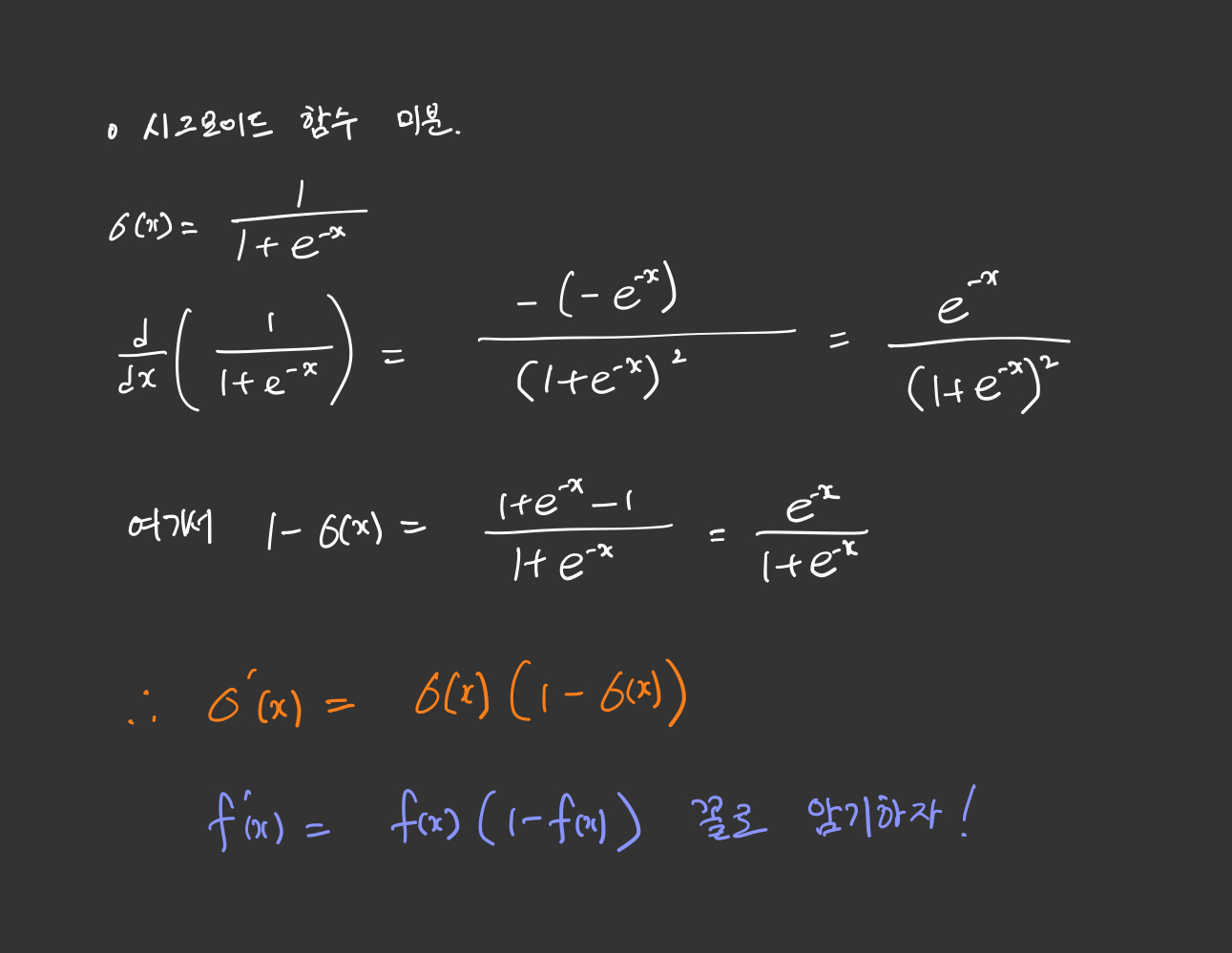
시그모이드 함수를 미분해야할 상황이 자주 생기므로, 기억하면 좋을 것 같습니다.

두번째 항을 계산해보면 $o_{1}$ 에 대한 $z_{3}$ 방향으로의 편미분이므로

\[\frac{∂o_{1}}{∂z_{3}}=o_{1}\text{×}(1-o_{1})=0.60944600(1-0.60944600)=0.23802157\]

마지막으로 세번째 항은 그냥 화살표 방향만 따라서 뒤로 가면 되므로 $h_{1}$ 갑과 동일합니다. ($z_{3}$ 에 대하여 $W_{5}$ 방향으로의 편미분)

\[\frac{∂z_{3}}{∂W_{5}}=h_{1}=0.51998934\]

이제 우변의 모든 항을 계산해주면,

\[\frac{∂E_{total}}{∂W_{5}} = 0.20944600 \text{×} 0.23802157 \text{×} 0.51998934 = 0.02592286\]

이제 앞서 배웠던 Gradiendt Descent(경사 하강법)을 통해 가중치를 업데이트 할 때가 왔습니다. 하이퍼파라미터에 해당되는 학습률 $\alpha$ 는 0.5라고 가정하겠습니다.

업데이트 되는 새로운 녀석들을 지수쪽에 +로 표시하겠습니다.

\[W_{5}^{+}=W_{5}-α\frac{∂E_{total}}{∂W_{5}}=0.45- 0.5 \text{×} 0.02592286=0.43703857\]

이와 같은 원리로 $W_{6}^{+},\ W_{7}^{+},\ W_{8}^{+}$ 를 계산할 수 있습니다.

역전파 2단계(BackPropagation Step2)

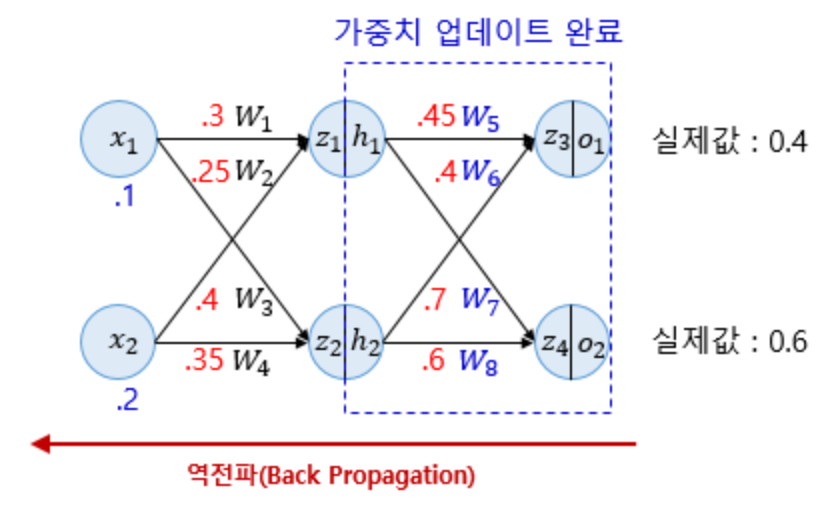
1단계를 완료했다면, 이제 입력층의 방향으로 2단계를 진행하여야합니다. 2단계에서도 1단계와 같은 매커니즘으로 계산을 진행해주면 됩니다.

이번에도 $W_{1}$ 에 대해서 먼저 업데이트를 진행해보겠습니다. 업데이트를 하기 위해서는 $\frac{∂E_{total}}{∂W_{1}}$ 를 계산해야합니다.

위에서 했던 것 처럼 미분의 연쇄 법칙을 이용하면

\[\frac{∂E_{total}}{∂W_{1}} = \frac{∂E_{total}}{∂h_{1}} \text{×} \frac{∂h_{1}}{∂z_{1}} \text{×} \frac{∂z_{1}}{∂W_{1}}\]

우변의 첫째 항인 $\frac{∂E_{total}}{∂h_{1}}$ 을 조금 더 풀어서 쓰면

\[\frac{∂E_{total}}{∂h_{1}} = \frac{∂E_{o1}}{∂h_{1}} + \frac{∂E_{o2}}{∂h_{1}}\]

이제 다시 위의 식의 우변의 두 항을 각각 구해보겠습니다.

\[\frac{∂E_{o1}}{∂h_{1}} = \frac{∂E_{o1}}{∂z_{3}} \text{×} \frac{∂z_{3}}{∂h_{1}} = \frac{∂E_{o1}}{∂o_{1}} \text{×} \frac{∂o_{1}}{∂z_{3}} \text{×} \frac{∂z_{3}}{∂h_{1}}\] \[= -(target_{o1}-output_{o1}) \text{×} o_{1}\text{×}(1-o_{1}) \text{×} W_{5}\] \[= 0.20944600 \text{×} 0.23802157 \text{×} 0.45 = 0.02243370\]

이와 같은 원리로 $\frac{∂E_{o2}}{∂h_{1}}$ 도 구해보면

\[\frac{∂E_{o2}}{∂h_{1}} = \frac{∂E_{o2}}{∂z_{4}} \text{×} \frac{∂z_{4}}{∂h_{1}} = \frac{∂E_{o2}}{∂o_{2}} \text{×} \frac{∂o_{2}}{∂z_{4}} \text{×} \frac{∂z_{4}}{∂h_{1}} = 0.00997311\] \[\frac{∂E_{total}}{∂h_{1}} = 0.02243370 + 0.00997311 = 0.03240681\]

이제 첫번째 항을 다 구했습니다. 나머지 두 항도 마저 구하면

\[\frac{∂h_{1}}{∂z_{1}} = h_{1}\text{×}(1-h_{1}) = 0.51998934(1-0.51998934)=0.24960043\] \[\frac{∂z_{1}}{∂W_{1}} = x_{1} = 0.1\]

즉, 모두 더해주면

\[\frac{∂E_{total}}{∂W_{1}} = 0.03240681 \text{×} 0.24960043 \text{×} 0.1 = 0.00080888\]

이제 앞서 배웠던 경사 하강법을 통해 가중치를 업데이트 할 수 있습니다.

\[W_{1}^{+}=W_{1}-α\frac{∂E_{total}}{∂W_{1}}=0.1- 0.5 \text{×} 0.00080888=0.29959556\]

이와 같은 원리로 $W_{2}^{+},\ W_{3}^{+},\ W_{4}^{+}$ 도 마저 구해주면

\[\frac{∂E_{total}}{∂W_{2}} = \frac{∂E_{total}}{∂h_{1}} \text{×} \frac{∂h_{1}}{∂z_{1}} \text{×} \frac{∂z_{1}}{∂W_{2}} → W_{2}^{+}=0.24919112\] \[\frac{∂E_{total}}{∂W_{3}} = \frac{∂E_{total}}{∂h_{2}} \text{×} \frac{∂h_{2}}{∂z_{2}} \text{×} \frac{∂z_{2}}{∂W_{3}} → W_{3}^{+}=0.39964496\] \[\frac{∂E_{total}}{∂W_{4}} = \frac{∂E_{total}}{∂h_{2}} \text{×} \frac{∂h_{2}}{∂z_{2}} \text{×} \frac{∂z_{2}}{∂W_{4}} → W_{4}^{+}=0.34928991\]

결과 확인

이제 다시 새로 업데이트 된 가중치들로 순전파를 계산하여 오차가 감소했는지 확인해보면

마크다운 수식은 정말 ^^

마지막 연산은 사진으로 대체했습니다.

기존의 오차보다 오차가 조금이지만 줄어든 것을 확인할 수 있습니다. 이렇게 인공 신경망의 학습은 오차를 최소화하는 가중치를 찾는 목적으로 순전파와 역전파를 반복하는 것을 말합니다.

XOR - 다층 퍼셉트론으로 구현하기

기본설정을 해줍니다.

import torch
import torch.nn as nn

GPU 연산이 가능하신분들은 GPU연산을 하도록하고, 저는 맥북이라서 CPU를 사용하겠습니다.

device = 'cuda' if torch.cuda.is_available() else 'cpu'

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

XOR 문제를 풀기위한 예제의 입력과 출력값입니다.

X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

이제 다층 퍼셉트론을 설계합니다. 우리가 설계해볼 퍼셉트론은 입력층, 은닉층1, 은닉층2, 은닉층3, 출력층을 가지는 퍼셉트론입니다.

model = nn.Sequential(
          nn.Linear(2, 10, bias=True), # input_layer = 2, hidden_layer1 = 10
          nn.Sigmoid(),
          nn.Linear(10, 10, bias=True), # hidden_layer1 = 10, hidden_layer2 = 10
          nn.Sigmoid(),
          nn.Linear(10, 10, bias=True), # hidden_layer2 = 10, hidden_layer3 = 10
          nn.Sigmoid(),
          nn.Linear(10, 1, bias=True), # hidden_layer3 = 10, output_layer = 1
          nn.Sigmoid()
          ).to(device)

퍼셉트론 구조를 그림으로 표현하면 다음과 같습니다.

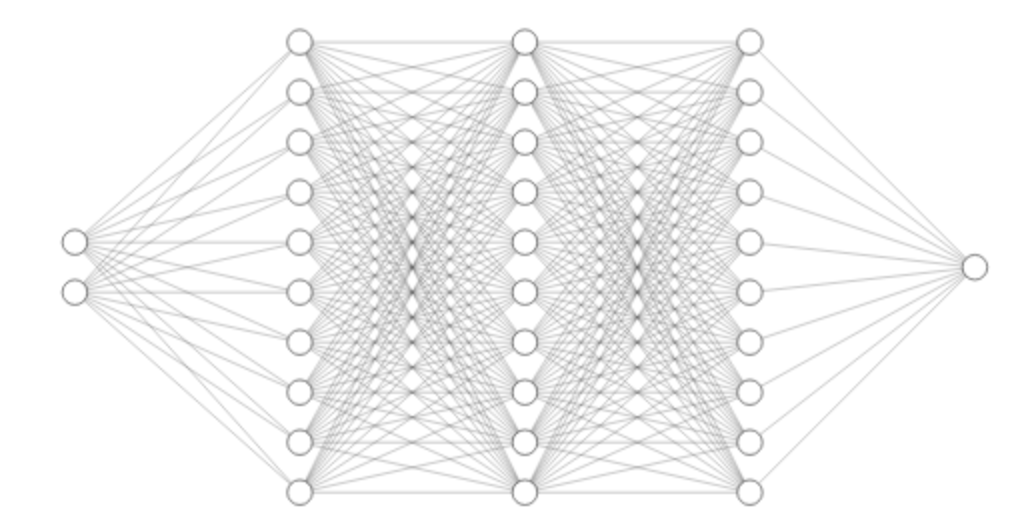
이제 비용함수와 옵티마이저를 선언합니다. nn.BCELoss()는 이진 분류에서 사용하는 크로스엔트로피 함수입니다.

criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)  # modified learning rate from 0.1 to 1

총 10,001번의 에포크를 수행합니다. 각 에포크마다 역전파가 수행된다고 보면 되겠습니다.

for epoch in range(10001):
    optimizer.zero_grad()
    # forward 연산
    hypothesis = model(X)

    # 비용 함수
    cost = criterion(hypothesis, Y)
    cost.backward()
    optimizer.step()

    # 100의 배수에 해당되는 에포크마다 비용을 출력
    if epoch % 100 == 0:
        print(epoch, cost.item())

비용이 최소화 되는 방향으로 가중치와 편향이 업데이트 됩니다. 사실 지금까지 모르고 사용해왔던 코드들인데 알고나니 느낌이 조금 다른 것 같습니다 ㅋㅋㅋㅋ

위 사진은 직접 주피터 노트북으로 돌려본 결과 값입니다. 100배수 마다 손실값이 줄어드는 것을 보실 수 있습니다.

끝!

참고문헌