Lec 09-3,4: Dropout & Batch Normalization

딥러닝 공부 15일차

이전에 Overfitting(과적합)을 방지할 수 있는 방법을 소개했었습니다. 다시 몇가지 적어보면

• More training data
• Reduce the number of features
• Regularization
• Dropout

과적합을 방지하는 방법 중 하나인 Dropout에 대해서 오늘 공부해보겠습니다.

Dropout

dropout은 쉽게말하면 매 층마다 어떠한 확률로 일부는 버리고 남은 나머지들로 학습해나가는 것을 말합니다.

즉, 신경망의 일부를 사용하지 않는 방법입니다.

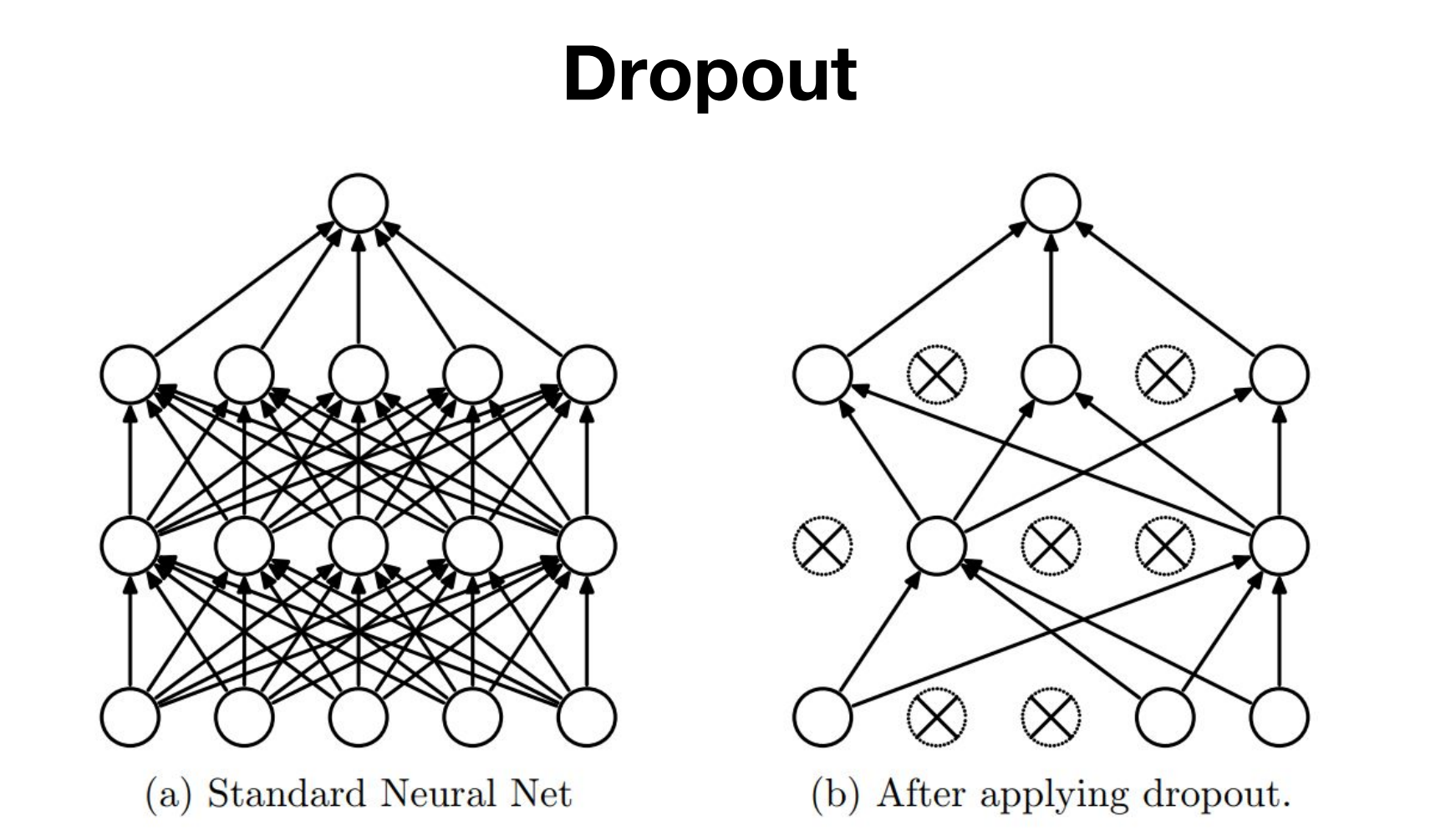
드롭아웃은 신경망 학습시에만 사용하고, 예측시에는 사용하지 않습니다.

학습시에 인공 신경망이 특정 뉴런 또는 특정 조합에 너무 의존적이게 되는 것을 방지해주고, 매번 랜덤 선택으로 뉴런들을 사용하지 않으므로 과적합을 방지해줍니다.

코드로는 다음과 같이 사용할 수 있습니다.

...

# nn layers
linear1 = torch.nn.Linear(784, 512, bias=True)
linear2 = torch.nn.Linear(512, 512, bias=True)
linear3 = torch.nn.Linear(512, 512, bias=True)
linear4 = torch.nn.Linear(512, 512, bias=True)
linear5 = torch.nn.Linear(512, 10, bias=True)
relu = torch.nn.ReLU()
dropout = torch.nn.Dropout(p=drop_prob)

# model
model = torch.nn.Sequential(linear1, relu, dropout,
 linear2, relu, dropout,
 linear3, relu, dropout,
 linear4, relu, dropout,
 linear5).to(device)

딥러닝공부 16일차

앞서 배웠던 Gradient Vanishing 현상과 Gradient Exploding(vanishing과 반대되는 현상으로, 기울기값이 너무 클 경우 발생) 현상을 해결할 수 있는 방법으로

• Activation fuction을 바꾸기
• Careful Initialization
• 학습률을 낮추기

와같은 방법들이 있습니다. 하지만 이 외에 Batch Normalization 이라는 방법이 있습니다. 오늘은 이 배치노말라이제이션에 대해서 알아보겠습니다.

Batch Normalization

ReLU 계열의 함수와 He 초기화를 사용하는 것만으로도 어느정도 기울기 소실과 폭주를 예방할 수 있지만, 100%는 아니기 때문에, 또 다른 방법으로 제안된 것이 배치 정규화입니다.

배치 정규화(Batch Normalization)은 인공신경망의 각 층에 들어가는 입력을 평균과 분산으로 정규화하여 학습을 효율적으로 만드는 방법입니다.

Internal Covariate Shift(내부 공변량 변화)

내부 공변량 변화란 학습 과정에서 층 별로 입력 데이터 분포가 달라지는 현상을 말합니다. 즉, 이전 층들의 학습에 의해 이전 층의 가중치가 바뀌게되면, 현재 층에 전달되는 입력 데이터의 분포가 현재 층이 학습했던 시점의 분포와 차이가 발생하게 됩니다.

배치정규화를 제안한 논문에서는 기울기 소실,폭주 등의 딥러닝 모델의 불안정성이 층마다 입력의 분포가 달라지기 때문이라고 주장합니다.

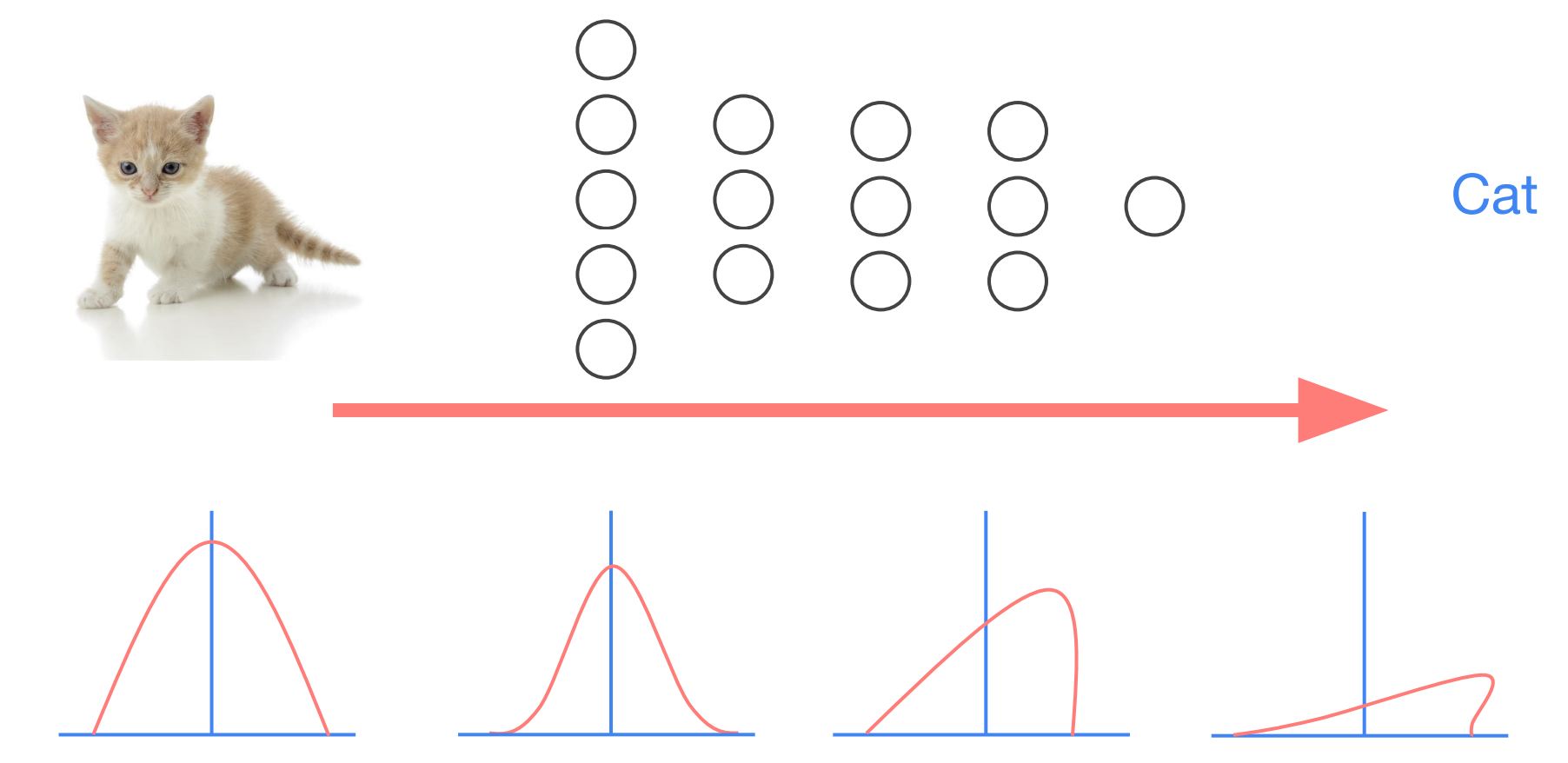
예를 들어서 사진을 보고 고양이인지 아닌지 분류하는 분류기를 학습시킨다고 가정했을 때, 층 하나를 지날 때마다, 사진의 그래프처럼 문제가 발생하게 됩니다.

배치 정규화는 말 그대로 한 번에 들어오는 배치 단위로 정규화하는 것을 말합니다. 배치 정규화는 각 층에서 활성화 함수를 통과하기 전에 수행됩니다.

순서를 요약하면 다음과 같습니다.

1. 입력에 대해 평균을 0으로 만들고, 정규화를 한다.
2. 정규화된 데이터에 대해서 스케일과 시프트를 수행한다.

배치 정규화의 식을 살펴보면 다음과 같습니다. $BN$은 배치 정규롸를 의미합니다.

input: 미니 배치 $B = {x^{(1)}, x^{(2)}, …, x^{(m)}}$

output: $y^{(i)} = BN_{γ, β}(x^{(i)})$

\[μ_{B} ← \frac{1}{m} \sum_{i=1}^{m} x^{(i)} \text{ 👉 미니 배치에 대한 평균}\] \[σ^{2}_{B} ← \frac{1}{m} \sum_{i=1}^{m} (x^{(i)} - μ_{B})^{2}\text{ 👉 미니 배치에 대한 분산}\] \[\hat{x}^{(i)} ← \frac{x^{(i)} - μ_{B}}{\sqrt{σ^{2}_{B}+ε}}\text{ 👉 정규화}\] \[y^{(i)} ← γ\hat{x}^{(i)} + β = BN_{γ, β}(x^{(i)}) \text{ 👉 스케일 조정과 시프트}\]

• $m$은 미니 배치에 있는 샘플의 수
• $μ_{B}$는 미니 배치 $B$에 대한 평균.
• $σ_{B}$는 미니 배치 $B$에 대한 표준편차.
• $\hat{x}^{(i)}$은 평균이 0이고 정규화 된 입력 데이터.
• $ε$은 분모가 0이 되는 것을 막는 작은 수. 보편적으로 $10^{-5}$
• $\gamma$는 정규화 된 데이터에 대한 스케일 매개변수로 학습 대상
• $\beta$는 정규화 된 데이터에 대한 시프트 매개변수로 학습 대상
• $y^{(i)}$는 스케일과 시프트를 통해 조정한 $BN$의 최종 결과
  

배치 정규화의 장점은 다음과 같습니다.

• 시그모이드나 하이퍼블릭탄젠트 함수를 사용해도 기울기 소실 문제가 크게 개선됨.
• 가중치 초기화에 덜 민감해짐.
• 훨씬 큰 학습률을 사용할 수 있어 학습 속도가 개선됨.
• 과적합을 방지하는 효과가 미미하지만 존재.
  

배치 정규화의 단점은 다음과 같습니다.

• 미니 배치 크기에 의존적이다.
• RNN에 적용하기 어렵다.

끝!

참고문헌1, 참고문헌2