Optimizer 총정리 : GD, SGD, Momentum, Adagrad, RMSProp, Adam
Adam 은 Momentum 방식과 RMSProp 방식의 합입니다. GD부터 순차적으로 하나씩 뜯어보면서 Adam Optimizer에 대해서 알아보겠습니다.
GD(gradient descent)
GD복습하기 👈 클릭!
Gradient Descent는 학습률에 따라 발산하거나 Local Minimum에 빠지기 쉽다는 단점이 있습니다.
또한 Convex(볼록) 함수에서는 잘 작동하지만 Non-Convex(비볼록) 함수에서는 안장점을 최저점이라 생각하고 벗어나지 못하는 단점이 있습니다.
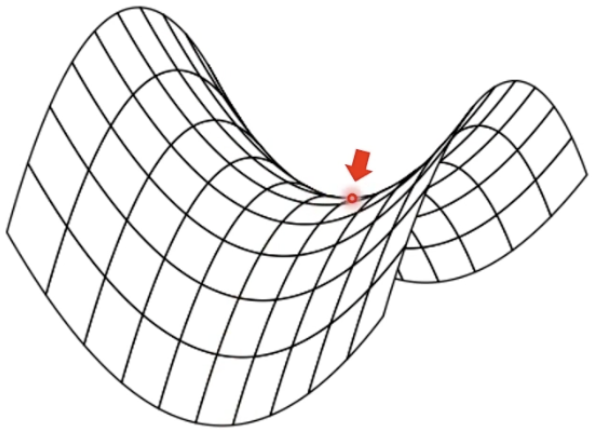
이러한 안장점에서는 미분계수가 0이 나오기 때문에 학습이 더 이상 진행되지 않게 됩니다.
또한 GD는 한번에 epoch에 모든 학습데이터를 학습하기 때문에 컴퓨터에 큰 부담을 지우게 됩니다. 그래서 나온 Optimizer가 Batch_size 개념이 탑재된 Stochastic Gradient Descent인 SGD방법입니다.
SGD
SGD복습하기 👈 클릭!
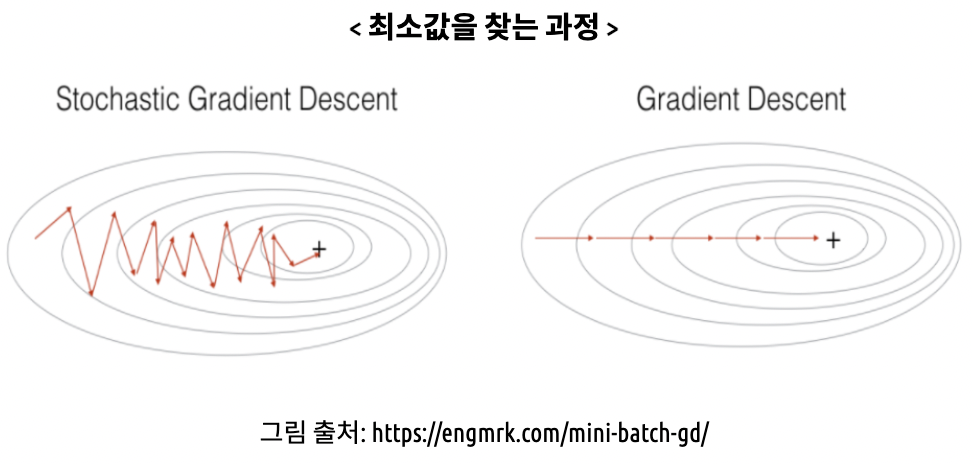
SGD는 GD의 단점을 보와하기위헤서 위 그림과 같이 전체 학습 데이터셋에서 Batch_size 만큼 무작위로 뽑아서 그 만큼을 한번에 epoch으로 학습시키는 방법입니다.
하지만 충분한 반복이 되지 않는다면 손실함수의 최저점을 찾지 못할 수도 있다는 단점과, 위아래로 요동치듯이 움직이기 때문에 노이즈가 심하다는 단점이 있습니다.
즉, 비등방성 함수의 경우에 학습이 비효율적인 단점이 존재합니다.
SGD with Python Numpy
class SGD: # 확률적 경사 하강법
def __init__(self, lr=0.01): #학습률 = 0.01
self.lr = lr
def update(self, params, grads): # 가중치, 미분기울기 딕셔너리
for key in params.keys(): # 가중치 키 값 업데이트 과정
params[key] -= self.lr * grads[key] # 가중치 키(값) -= 손실함수 기울기 * 학습률, 최저점 찾는 과정
Momentum
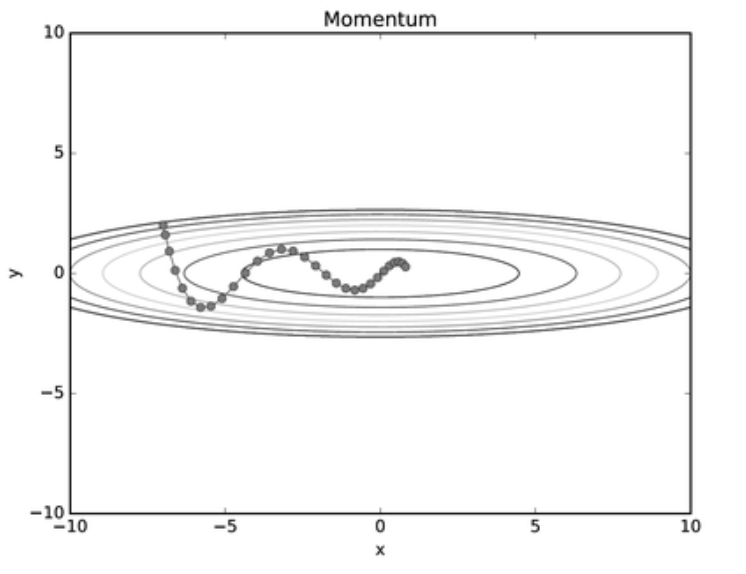
위의 SGD의 단점을 보완한 방법으로 Momentum 방식이 등장하였습니다.
Momentum의 사전적 정의는 외부의 힘을 받지 않는 한, 정지해 있거나 운동상태를 지속하려는 성질을 말합니다. 즉, 관성의 성질입니다.

Momentum에서는 가중치 W의 갱신 방법으로 이전 가중치에 속도가 더해지는 방식을 사용합니다.
속도 v는 {$\alpha$(관성계수) X 이전 타임스텝에서의 속도벡터} 에서 손실함수의 기울기에 학습률만큼 곱해진만큼 뺀만큼이 속도 매개변수로 갱신되게 됩니다.
Momentum with Python Numpy
Momentum을 파이썬 코드로 구현해보면 아래와 같습니다.
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr #학습률
self.momentum = momentum #관성계수
self.v = None #초기 속도값 None
def update(self, params, grads):
# 업데이트, params, grads 두 가지 딕셔너리
if self.v is None: #학습시작시
self.v = {} #빈 딕셔너리 생성
for key, val in params.items():
#파라미터 params(가중치) 딕셔너리의 키, 값 쌍 얻기
self.v[key] = np.zeros_like(val)
# v딕셔너리의 키값에 영행렬로 이루어진 val(값) 할당
for key in params.keys(): # params의 키값 개수만큼 반복
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
# 속도 키값 = 알파*V(이전스텝) - 학습률*손실함수기울기 (계속 업데이트)
params[key] += self.v[key] #params키(가중치) += 속도 (계속 업데이트)
Adagrad
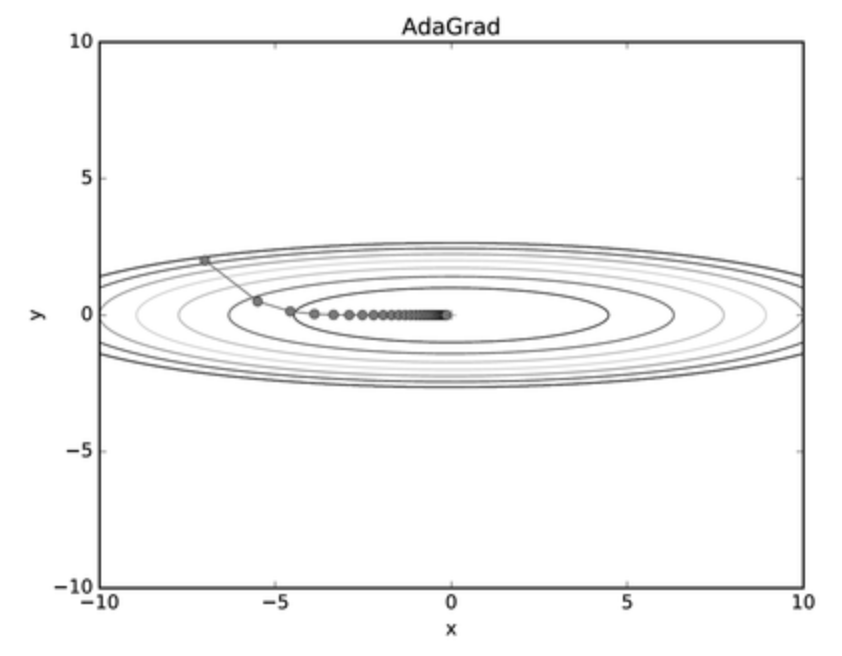
Adaptive Gradient의 약자로, 적응적 기울기라고 불립니다. 매개변수(Feature)마다 중요도, 크기 등이 제각각이기 때문에 모든 매개변수별로 같은 학습률을 적용하는 것은 비효율적입니다.
그러므로 Adagrad에서는 Feature별로 학습률을 다르게 조절하는 것이 특징입니다.
Adagrad의 수식은 다음과 같습니다.
- $g_{t}$ : t번째 time step 까지의 기울기
- $\epsilon$ : 분모가 0이 되는 것을 방지하기 위한 값 $\approx$ $10^{-8}$
- $\eta$ : 학습률 $\approx$ 0.001
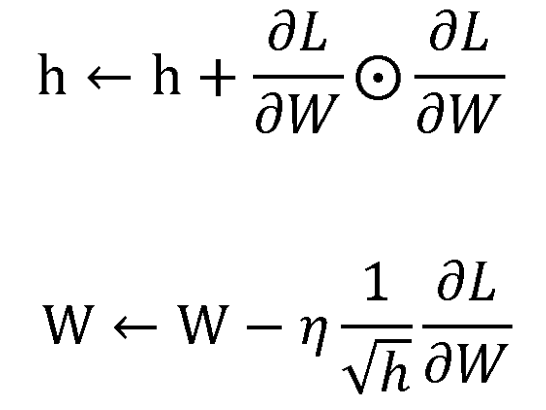
@ 기호는 행렬의 원소별 곱셈입니다. h는 기존 기울기 값을 제곱하여 계속 더해주고, 가중치 W를 갱신할 때는 제곱근의 역수에 학습률과 손실함수의 기울기만큼이 곱해져서 빼주게 됩니다.
이렇게 되면 매개변수 원수중에서 많이 갱신된(기울기 변화가 큰) 변수는, h값이 커지고, 가중치의 변화는 적어지게 됩니다. 즉, 가중치 갱신이 매개변수의 원소마다 다르게 적용된다는 것을 말합니다.
Adagrad는 과거의 기울기를 제곱하여 계속 더해가기 때문에, 학습이 오래 진행될수록 갱신 강도가 약해지게됩니다. 그래서 어느 순간부터 갱신량이 0이되어 갱신하지 않게되는 단점이 존재합니다.
아래는 넘파이로 구현한 Adagrad 코드입니다.
Adagrad with Python Numpy
class Adagrad: # Adagrad 구현
def __init__(self, lr=0.01): # 학습률 = 0.01
self.lr = lr
self.h = None # 초기 h값
def update(self, params, grads): # 업데이트
if self.h is None: # h가 None이면,
self.h = {} # h 딕셔너리 생성
for key, val in params.items(): #가중치 아이템(key, val) 꺼내오기
self.h[key] = np.zeros_like(val) # h의 key에 val 모양의 영행렬 할당
for key in params.keys(): # 가중치 key 하나씩 꺼내기
self.h[key] += grads[key] * grads[key] # h값에 미분값 행렬 원소별 곱셈
params.[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7) # 위 공식사진 참고
RMSProp
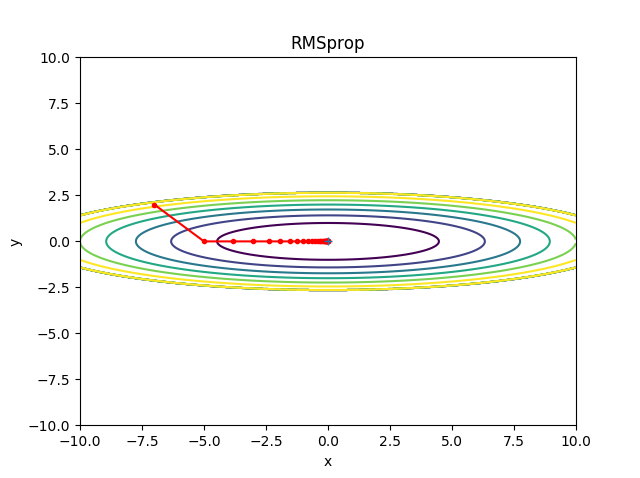
위에서 설명한 Adagrad의 단점을 보완하기 위해서 과거의 모든 기울기를 균일하게 더하지 않고 먼 과거의 기울기는 조금씩, 최근의 기울기는 크게 반영하는 기법이 만들어졌습니다. 이를 지수이동평균, Exponential Moving Average, EMA 라고 하고 과거 기울기의 반영 규모를 기하급수적으로 감소시킵니다.
\[g_{t} = \gamma g_{t-1} + (1-\gamma)(\nabla f(x_{t-1}))^{2}\] \[x_{t} = x_{t-1} - \frac{\eta}{\sqrt{g_{t} + \epsilon}} \cdot \nabla f(x_{t-1})\]- $g_{t}$ : t번째 time step까지의 기울기 누적 크기
- $\gamma$ : 지수이동평균의 업데이트 계수
- $\epsilon$ : 분모가 0이 되는 것을 방지하기 위한 작은 값 $\approx$ $10^{-6}$
- $\eta$ : 학습률
딱 Adagrad 방식에 지수이동평균계수만 추가되어 곱해진 것을 확인하실 수 있습니다.
RMSProp with Python Numpy
아래는 Numpy로 구현한 RMSProp 코드입니다.
class RMSProp:
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
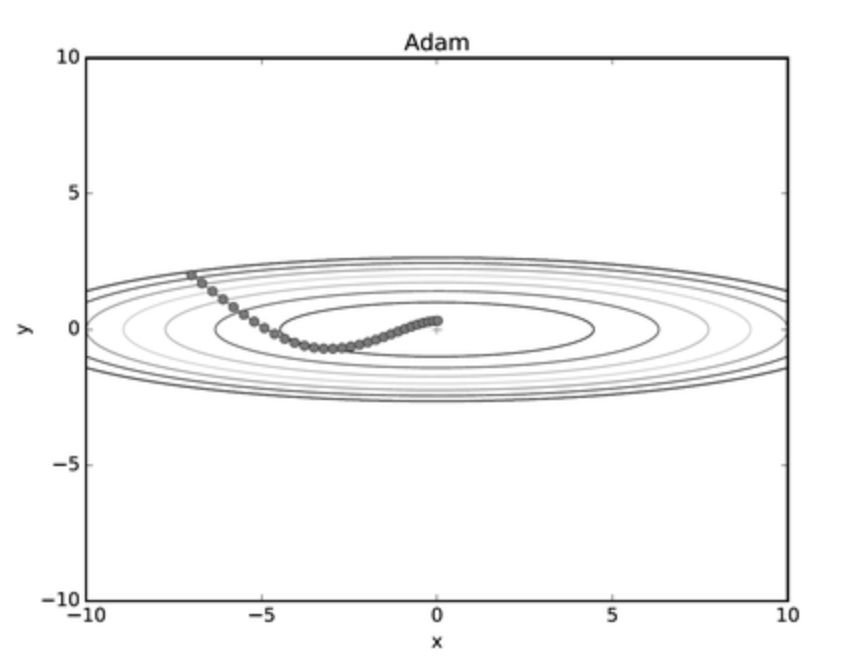
Adaptive Moment Estimation(Adam)은 딥러닝 최적화 기법 중 하나로써 Momentum 방식과 Adagrad(관점에따라 RMSProp이라고 하는 사람도 많습니다)
\[m_{t} = \beta_{1} m_{t-1} + (1 - \beta_{1}) \nabla f(x_{t-1})\] \[g_{t} = \beta_{2} g_{t-1} + (1-\beta_{2})(\nabla f(x_{t-1}))^{2}\] \[\hat{m_{t}} = \frac{m_{t}}{1-\beta^{t}_{1}}, \hat{g_{t}} = \frac{g_{t}}{1-\beta^{t}_{2}}\] \[x_{t} = x_{t-1} - \frac{\eta}{\sqrt{\hat{g_{t}} + \epsilon}} \cdot \hat{m_{t}}\]사실 Adagrad에서 조금 더 발전된 것이 RMSProp이라서 두개 중 뭐가 합쳐졌다로 싸우는건 의미가 없다고 생각듭니다. 이글에서는 RMSProp으로 말하겠습니다.
- $\beta_{1}$ : Momentum의 지수이동 평균 $\approx$ 0.9
- $\beta_{2}$ : RMSProp의 지수이동 평균 $\approx$ 0.999
- $\hat{m},\hat{g}$ : 학습 초기 시 $m_{t}, g_{t}$ 가 0이 되는 것을 방지하기 위한 보정 값
- $\epsilon$ : 분모가 0이 되는것을 방지하기 위한 작은 값 $\approx$ $10^{-8}$
- $\eta$ : 학습률 $\approx$ 0.001
Python code 로 구현한 Adam
class Adam: #Adam 구현
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): #학습률=0.001, 베타1=0.9, 베타2=0.999
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0 # 타임스텝을 세주기 위한 변수
self.m = None #
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
이상으로 Optimizer에 관해서 총정리를 해보았습니다~

댓글남기기