DSP(디지털신호처리) - Sampling & Quantization
T acdemy_디지털신호처리 기초1
DSP
자료들은 티아카데미, 도승현 강사님의 자료에서 따왔음을 알립니다.
현재 인공지능 딥러닝분야에서 이미지 처리쪽은 정말 눈부시게 발전을 해온 반면, 음성쪽은 그렇지가 않았습니다.
그 이유는 음성데이터에는 많은 잡음들이 있고, 그러한 음성 데이터는 연속적인 아날로그 신호이기 때문에, 이를 컴퓨터가 인식할 수 있게 디지털 신호로 바꾸어 주여야합니다.
하지만 이렇게 바꿔주는 과정도 만만치 않고, 이를 학습하는 과정도 실제로 쉽지 않다고 알고 있습니다.
예제 실습코드도 같이 진행하면서 공부하겠습니다.
!pip install torch
!pip install torchaudio
기본 필요파일을 다운로드 받아줍시다.
import librosa
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torchaudio
딥러닝 스터디에서 했던 MNIST 데이터셋처럼 오디오 데티어셋을 불러옵니다. 약6기가 정도 되므로 조금 기다려줍시다.
# tra
in_dataset = torchaudio.datasets.LIBRISPEECH("./", url="train-clean-100", download=True)
test_dataset = torchaudio.datasets.LIBRISPEECH("./", url="test-clean", download=True)
Computer가 소리를 인식하는 방식
연속적인 아날로그 신호를 표본화(Sampling), 양자화(Quantizing), 부호화(Encoding) 을 거쳐 디지털 신호(Binary Digital Signal) 로 변화시켜서 인식하게 됩니다.
샘플링이란? 1초의 연속적인 시그널을 몇개의 숫자로 표현할 것인가?
Sampling rate : 얼마나 잘게 쪼갤 것인가?
잘개 쪼갤수록 원본 데이터와 거이 가까워지기 떄문에 좋지만 Data의 양이 증가하게 됩니다. 만약 너무 크게 쪼개게 된다면, 원본 데이터로 재구성(reconstruct)하기 힘들어 질 것입니다.
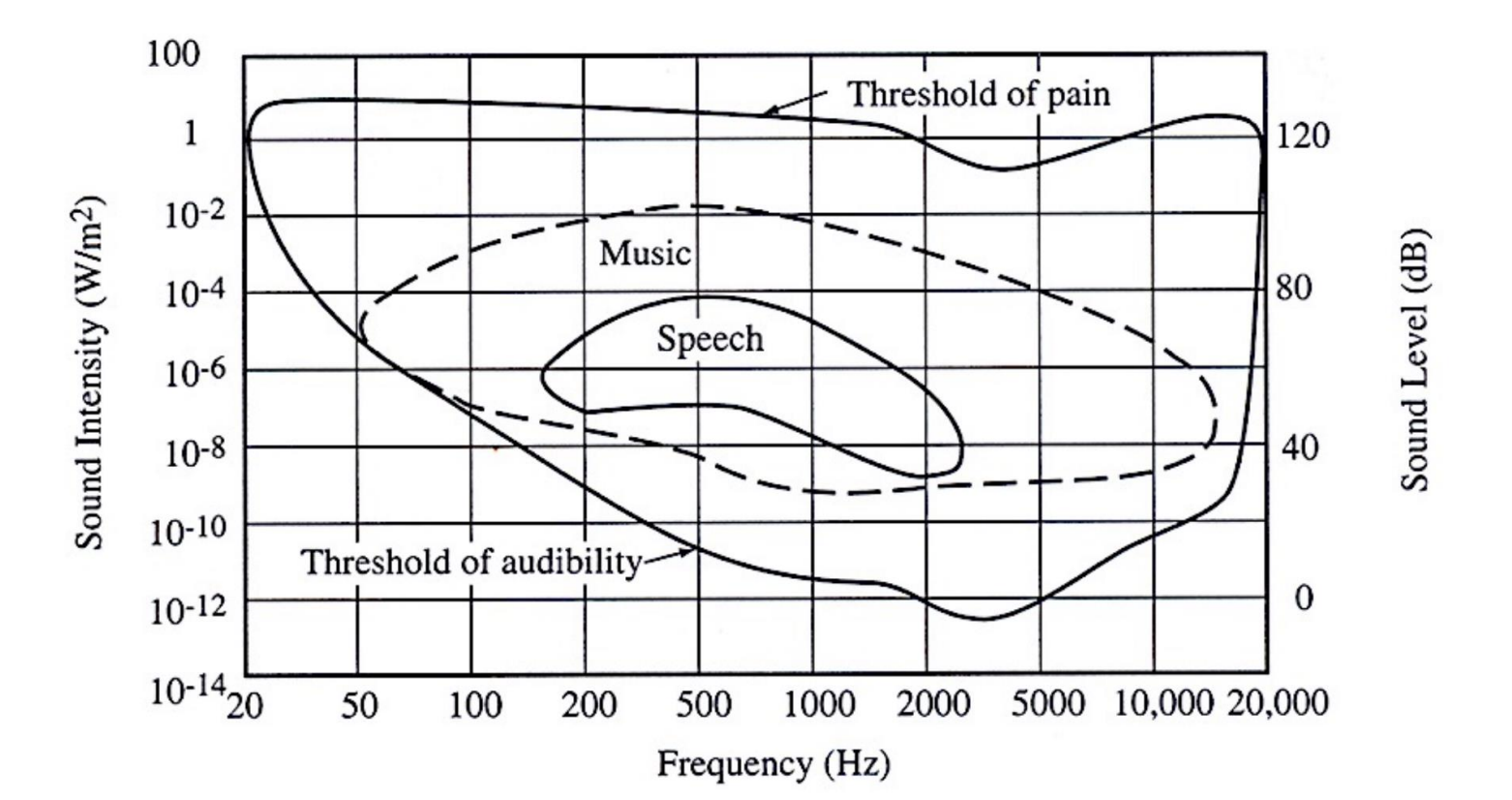
어떻게 Sampling Rate를 정하나요?
나이키스트-섀넌 표본화 에 따르면 A/D를 거치고, D/A로 복원하기 위해서는 표본화된 신호의 최대 주파수가 두배 보다 더 클 때 가능하다고 합니다.
일반적으로 사용되는 주파수 영역대는 16KHz(speech), 22.05KHz, 44.1KHz(music) 입니다.
$𝑓𝑠>2𝑓𝑚$ 여기서 $𝑓𝑠$는 sampling rate, 그리고 $𝑓𝑚$은 maximum frequency를 말합니다.
위 그림으로 예를 들면 사람의말의 주파수 범위의 최대값이 2000Hz 부근이니까 Sample Rate가 4000Hz 이하로는 내려가면 안되겠다 정도로 파악하면 되겠습니다.
오디오 파일이 다운이 완료된 후, 예시로 아래와 같은 데이터셋을 출력해보면
test_dataset[0]
첫번째 데이터를 출력해보면
(tensor([[0.0003, 0.0003, 0.0004, …, 0.0021, 0.0021, 0.0016]]),
16000,
‘HE HOPED THERE WOULD BE STEW FOR DINNER TURNIPS AND CARROTS AND BRUISED POTATOES AND FAT MUTTON PIECES TO BE LADLED OUT IN THICK PEPPERED FLOUR FATTENED SAUCE’,
1089,
134686,
0)
텐서의 모양이 소리라고 보면 되고, 두번째의 16000이 샘플레이트라고 보면 되겠습니다. 세번째가 실제 말을 적어 놓은 것이고, (뒤에 세가지는 아직 잘 모르겠습니다 ㅠㅠ…)
test_dataset[0][0].shape #소리 데이터, 샘플레이트
위 코드를 출력해보면,
torch.Size([1, 166960])
이것으로 보아 오디오파일은 3차원텐서느낌이지 않나 생각하였습니다. 왜 느낌이라고 했냐면 실제로 저장된 값이 저 위에 영어나 숫자처럼 모두 숫자로 이루어져있는 것이 아니기 때문입니다.
하지만 이제 그냥 3차원 텐서라고 말하겠습니다. 3차원 텐서이기 때문에 뒤에서 사용할 Librosa 함수에는 위의 166960 같은 값이 대입이 되어야하므로
test_dataset[0][0][0]
과 같은 꼴이 대입이 되어야합니다.
Librosa는 python에서 많이 쓰이는 음성 파일 분석 프로그램입니다.
Librosa를 쓰기 위해선 반드시 ffmpeg의 설치 여부를 확인해야 한다.그렇지 않으면 음성 파일을 로드하는 과정에서 에러가 발생하게 됩니다.
audioData = test_dataset[0][0][0]
sr = test_dataset[0][1]
print(audioData, audioData.shape)
tensor([0.0003, 0.0003, 0.0004, …, 0.0021, 0.0021, 0.0016]) torch.Size([166960])
len(audioData)
166960
len(audioData) / sr #duration이 나옴
음성 전체 길이를 샘플링 데이터로 나누면 duration, 즉 몇초의 사운드인지가 나오게 됩니다. 10.435
import IPython.display as ipd
ipd.Audio(audioData, rate=sr)
위 코드를 실행하면
‘HE HOPED THERE WOULD BE STEW FOR DINNER TURNIPS AND CARROTS AND BRUISED POTATOES AND FAT MUTTON PIECES TO BE LADLED OUT IN THICK PEPPERED FLOUR FATTENED SAUCE’ 를 들으실 수 있습니다.
Resampling
샘플링된 데이터를 다시금 더 높은 sampling rate 혹은 더 낮은 sampling rate로 다시 샘플링할수 있습니다. 이때는 일반적으로 interpolation(보간)을 할때는 low-pass filter를 사용합니다.(Windowed sinc function)
y_8k = librosa.resample(audioData.numpy(), sr, 8000) #torch에서 바로 import 해서 tensor로 되어 있음 -> numpy 붙이기
ipd.Audio(y_8k, rate=8000)
len(y_8k)
83480
y_2k = librosa.resample(audioData.numpy(), sr, 4000)
ipd.Audio(y_2k, rate=5000)
위 코드를 실행해보면 말이 빨라진 것을 확인하실 수 있습니다.
len(y_2k)
41740
Sound Representation
위에서 Sampling된 discrete한 데이터를 이제 우리는 표현이 가능합니다. 그렇다면 어떤 요소를 기반으로 저희가 데이터를 표현해야할까요?
첫번째는 시간의 흐름에 따라, 공기의 파동의 크기로 보는 Time-domain Representation 방법이 있습니다. 두번째는 시간에 따라서 frequency의 변화를 보는 Time-Frequency representation이 있습니다.
Time domain - Waveform Waveform의 경우에는 오디오의 자연적이 표현입니다. 시간이 x축으로 그리고 amplitude가 y축으로 표현이 됩니다.
import librosa.display
audio_np = audioData.numpy() #-> numpy로 바꾸기
fig = plt.figure(figsize = (14,5))
librosa.display.waveplot(audio_np[0:100000], sr=sr)
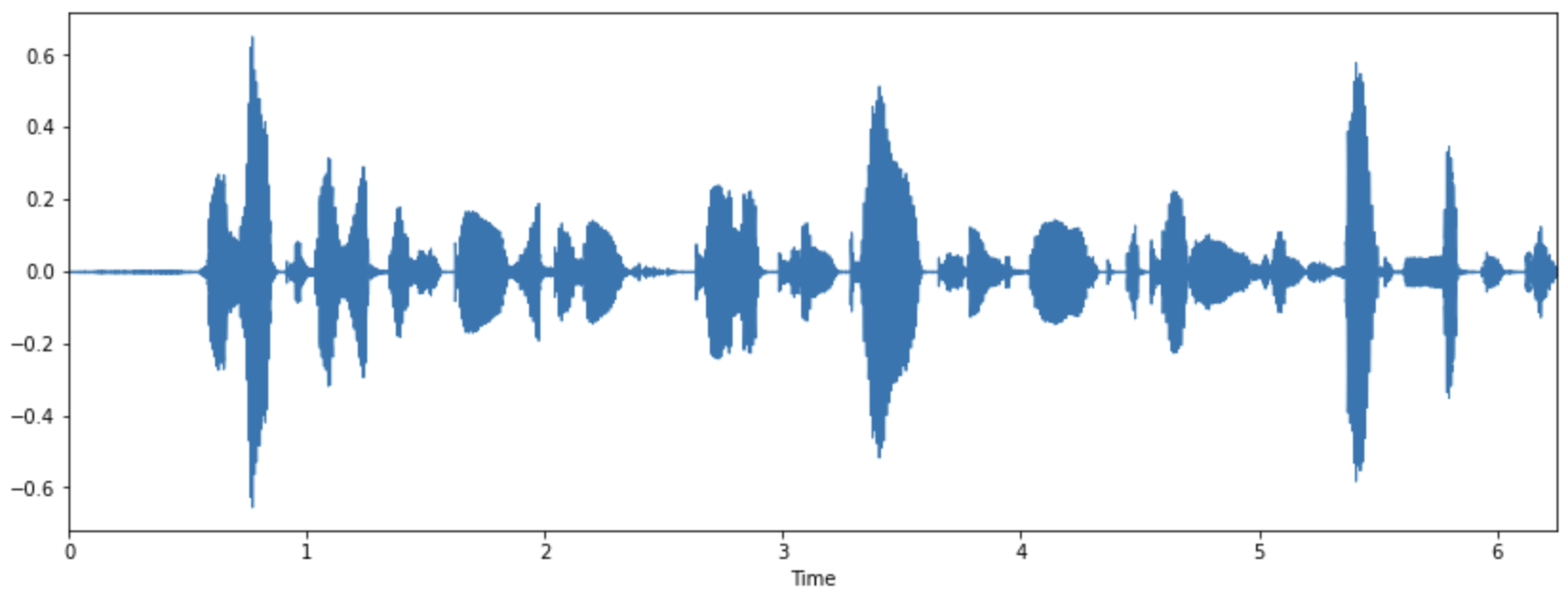
위 코드를 실행시켜서 얻은 소리의 파형입니다.
Nomalization & Quantization
양자화(Quantization)은 실제로 잘 사용하지는 않는다고 합니다.
시간의 기준이 아닌 실제 amplitude의 real valued 를 기준으로 시그널의 값을 조절합니다. Amplitude를 이산적인 구간으로 나누고, signal 데이터의 Amplitude를 반올림하게 됩니다.
그렇다면 이산적인 구간은 어떻게 나눌수 있을까요?, bit의 비트에 의해서 결정됩니다.
B bit의 Quantization : $−2^{𝐵−1} \sim 2^{𝐵−1}−1$
Audio CD의 Quantization (16 bits) : $−2^{15} \sim 2^{15}−1$
위 값들은 보통 -1.0 ~ 1.0 영역으로 scaling되기도 합니다.
audio_np = audioData.numpy()
normed_wav = audio_np / max(np.abs(audio_np))
ipd.Audio(normed_wav, rate=sr)
또한 양자화를 거치게되면
#quantization 하면 음질은 떨어지지만 light한 자료형이 된다.
Bit = 8
max_value = 2 ** (Bit-1)
quantized_8_wav = normed_wav * max_value
quantized_8_wav = np.round(quantized_8_wav).astype(int)
quantized_8_wav = np.clip(quantized_8_wav, -max_value, max_value-1)
ipd.Audio(quantized_8_wav, rate=sr)
정현파 (Sinusoid)
모든 신호는 주파수(frequency)와 크기(magnitude), 위상(phase)이 다른 정현파(sinusolida signal)의 조합으로 나타낼 수 있습니다.
퓨리에 변환은 조합된 정현파의 합(하모니) 신호에서 그 신호를 구성하는 정현파들을 각각 분리해내는 방법입니다.
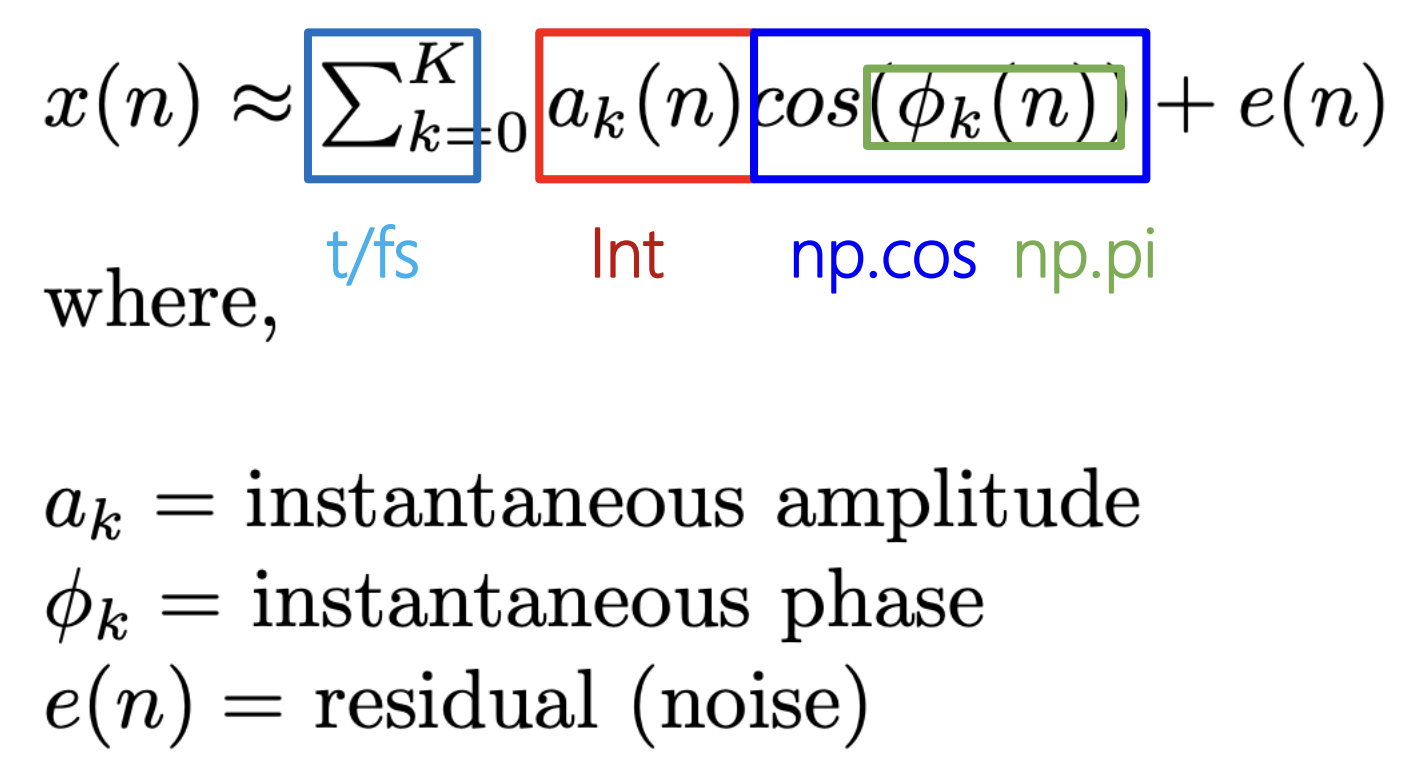
A = 0.9 #amplitude, 진폭
f = 440 # frequency, 진동수, 계이름 '라'
phi = np.pi/2
fs = 22050
t = 1 # 1초짜리 음악
#여러개의 정현파를 합치면 소리의 신호. 반대로 소리에서 정현파를 분리할 수 있다.
phi, fs는 아직 뭔지 모르겠네요 ㅠㅠ
def Sinusoid(A,f,phi,fs,t):
t = np.arange(0,t,1.0/fs)
x = A * np.cos(2*np.pi*f*t+phi)
return x
sin = Sinusoid(A,f,phi,fs,t)
ipd.Audio(sin, rate=fs)
위 코드를 실행하면 ‘라’ 음을 들을 수 있습니다.

댓글남기기